练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．（1）用辗转相除法求840与1 764 的最大公约数；
    （2）把666（7）化为十进制，把342（10）化为八进制．

    分析 （1）用辗转相除法求840与1764的最大公约数，写出1764=840×2+84，840=84×10+0，得到两个数字的最大公约数．
    （2）利用累加权重法，即可将七进制数转化为十进制，利用除K取余法即可将十进制数转化为八进制数．

    解答 解：（1）用辗转相除法求840与1764的最大公约数．
    1764=840×2+84，
    840=84×10+0
    ∴840与1764的最大公约数是84．
    （2）由题意，666（7）=6×72+6×71+6×70=342（10），
    342÷8=42…6
    42÷8=5…2
    5÷8=0…5
    可得：342（10）化成8进制是526（8）．

    点评 本题考查进制之间的转化，考查辗转相除法和更相减损术，熟练掌握进制之间的转化法则是解题的关键，这属于算法案例中的一种题目，解题时需要有耐心，认真计算，不要在数字运算上出错，本题是一个基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．设变量x、y满足约束条件$\left\{\begin{array}{l}3x+y-6≥0\\ x-y-2≤0\\ y-3≤0\end{array}\right.$，则目标函数z=4x+y的最小值为（　　）
    A．-6B．6C．7D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知命题p：2x2-9x+a＜0，命题q：x2-5x+6＜0，且非p是非q的充分条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．如图，在平面四边形ABCD中，AB=8，AD=5，CD=3$\sqrt{3}$，∠A=60°，∠D=150°，则BC=7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

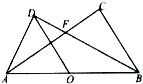    8．如图，△ABC与△ABD都是以AB为斜边的直角三角形，O为线段AB上一点，BD平分∠ABC，且OD∥BC．
    （1）证明：A，B，C，D四点共圆，且O为圆心；
    （2）AC与BD相交于点F，若BC=2CF=6，AF=5，求C，D之间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知数列{an}是等差数列，Sn为其前n项和，若平面上的三点A，B，C共线，且$\overrightarrow{OA}$=a4$\overrightarrow{OB}$+a97$\overrightarrow{OC}$，则S100=（　　）
    A．100B．101C．50D．51

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\frac{1}{3}$x3+x2+ax．若g（x）=$\frac{1}{e^x}$，对任意x1∈[$\frac{1}{2}$，2]，存在x2∈[$\frac{1}{2}$，2]，使f'（x1）≤g（x2）成立，则实数a的取值范围是（　　）
    A．$（-∞，\frac{{\sqrt{e}}}{e}-8]$B．$[\frac{{\sqrt{e}}}{e}-8，+∞）$C．$[\sqrt{2}，e）$D．$（-\frac{{\sqrt{3}}}{3}，\frac{e}{2}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若函数f（x）是定义在R上的偶函数，在（-∞，0）上对任意两个不相等的实数a，b总有$\frac{f（a）-f（b）}{a-b}$＞0，且f（2）=0，则使xf（x）＜0的x的取值范围是（　　）
    A．-2＜x＜2B．x＞2或-2＜x＜0C．-2＜x＜0D．x＜-2或x＞2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．如图程序输出结果为16

    查看答案和解析>>

    同步练习册答案