
分析 (1)进行数量积的坐标运算,并化简即可求得$f(x)=2sin(2x+\frac{π}{6})+4$,进而求出f(x)的最小正周期及对称中心;
(2)根据x的范围便可求出$2x+\frac{π}{6}$的范围,根据f(x)的解析式即可求出f(x)的值域.
解答 解:(1)$f(x)=\overrightarrow{a}•\overrightarrow{b}$
=$\sqrt{3}sin2x+3+2co{s}^{2}x$
=$\sqrt{3}sin2x+cos2x+4$
=$2sin(2x+\frac{π}{6})+4$;
∴f(x)的周期T=π;
令$2x+\frac{π}{6}=kπ$,k∈Z,则x=$\frac{kπ}{2}-\frac{π}{12}$,k∈Z;
∴图象对称中心为:$(\frac{kπ}{2}-\frac{π}{12},4)$,k∈Z;
(2)$f(x)=2sin(2x+\frac{π}{6})+4$;
$x∈[\frac{π}{12},\frac{7π}{12}]$,∴$2x+\frac{π}{6}∈[\frac{π}{3},\frac{4π}{3}]$;
∴f(x)∈[3,6];
即f(x)的值域为[3,6].
点评 考查数量积的坐标运算,二倍角的余弦公式,两角和的正弦公式,周期的计算公式,正弦函数的对称中心,以及正弦函数的图象.


科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等腰三角形 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\sqrt{3}$xy+y2=1 | B. | x2-xy+y2=1 | C. | x2+y2=1 | D. | x2+xy+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
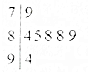 某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )
某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )| A. | 84 | B. | 85 | C. | 88 | D. | 89 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com