练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知集合A={x|x-1|≤2}，B={x|0＜x＜2}，则A∪B=（　　）
    A．AB．BC．∅D．R

    分析 求出A中不等式的解集确定出A，找出A与B的并集即可．

    解答 解：由A中不等式变形得：-2≤x-1≤2，
    解得：-1≤x≤3，即A={x|-1≤x≤3}，
    ∵B={x|0＜x＜2}，
    ∴A∪B={x|-1≤x≤3}=A，
    故选：A．

    点评 此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=$\frac{x}{lnx}$-ax．
    （Ⅰ）若函数f（x）在（1，+∞）上是减函数，求实数a的最小值；
    （Ⅱ）已知f′（x）表示f（x）的导数，若?x1，x2∈[e，e2]（e为自然对数的底数），使f（x1）-f′（x2）≤a成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若函数f（x）=2sin2x的图象向右平移φ（0＜φ＜π）个单位后得到函数g（x）的图象，若对满足|f（x1）-g（x2）|=4的x1、x2，有|x1-x2|的最小值为$\frac{π}{6}$，则φ=（　　）
    A．$\frac{π}{3}$B．$\frac{π}{6}$C．$\frac{π}{3}$或$\frac{2π}{3}$D．$\frac{π}{6}$或$\frac{5π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

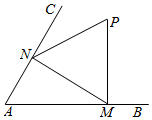    3．如图，已知∠BAC=$\frac{π}{3}$，正△PMN的顶点M、N分别在射线AB、AC上运动，P在∠BAC的内部，MN=2，M、P、N按逆时针方向排列，设∠AMN=θ．
    （1）求AM（用θ表示）；
    （2）当θ为何值时PA最大，并求出最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．α为实数，则“α=2kπ+$\frac{π}{4}$（k∈Z）”是“tanα=1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．（2x+5y）2016展开式中第k+1项的系数为（　　）
    A．$C_{2016}^k{2^{2016-k}}{5^{k-1}}$B．$C_{2016}^{k-1}{2^{2017-k}}{5^{k-1}}$
    C．$C_{2016}^{k-1}$D．$C_{2016}^k{2^{2016-k}}{5^k}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=|x+1|-2|x-1|．
    （1）求不等式f（x）≥1的解集；
    （2）求函数f（x）的图象与x轴围成的三角形的面积S．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．从某班5名男生和4名女生中选4人代表班级参加辩论赛，问
    （1）4人中至少有一名男生的选法有多少种？
    （2）若男生甲和女生乙只能有一人参赛且必然有一人参赛，有多少种选法？
    （3）辩论队员分为一辩，二辩，三辩，四辩，该班有多少种出赛阵容？
    （4）若男生甲和女生乙两人分担当一辩或四辩，则该班有多少种出赛阵容？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知正△ABC的边长为4，若在△ABC内任取一点，则该点到三角形顶点A、B、C距离都不小于2的概率为1-$\frac{\sqrt{3}}{6}$π．

    查看答案和解析>>

    同步练习册答案