
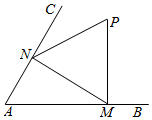
 如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.
如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.分析 (1)在△AMN中,由正弦定理可得:$\frac{AM}{sin(\frac{2π}{3}-θ)}$=$\frac{MN}{sin\frac{π}{3}}$,代入化简即可得出.
(II)在△AMP中,由余弦定理可得:AP2=AM2+22-4AMcos∠AMP,代入化简整理即可得出.
解答 解:(1)在△AMN中,由正弦定理可得:$\frac{AM}{sin(\frac{2π}{3}-θ)}$=$\frac{MN}{sin\frac{π}{3}}$,
∴AM=$\frac{4\sqrt{3}}{3}$$sin(\frac{2π}{3}-θ)$=$\frac{4\sqrt{3}}{3}$$sin(\frac{π}{3}+θ)$.
(II)在△AMP中,由余弦定理可得:
AP2=AM2+22-4AMcos∠AMP=$\frac{16}{3}si{n}^{2}(\frac{π}{3}+θ)$+4-$\frac{16}{3}sin(\frac{π}{3}+θ)$$cos(\frac{π}{3}+θ)$
=$\frac{8}{3}(1-cos(2θ+\frac{2π}{3}))$+4-$\frac{8\sqrt{3}}{3}$$sin(2θ+\frac{2π}{3})$
=$-\frac{8}{3}$$[\sqrt{3}sin(2θ+\frac{2π}{3})+cos(2θ+\frac{2π}{3})]$+$\frac{20}{3}$
=$\frac{20}{3}$-$\frac{16}{3}$$sin(2θ+\frac{5π}{6})$,θ∈$(0,\frac{2π}{3})$.
当且仅当$2θ+\frac{5π}{6}$=$\frac{3π}{2}$,即θ=$\frac{π}{3}$时,|AP|max=2$\sqrt{3}$.
点评 本题考查了正弦定理余弦定理、三角函数求值,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
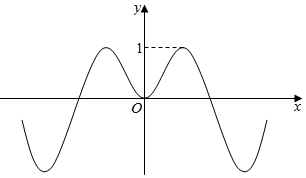
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10种 | B. | 60种 | C. | 125种 | D. | 243种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com