考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:数列{an}为等比数列,利用等比数列的性质得到a1a2012=a2a2011=…=a1006a1007,把已知的a1=1,a2012=4代入,求出a1a2012,a2a2011,…,a1006a1007的值,然后由函数解析式,利用求导法则求出f′(x),并把x=0代入导函数中,表示出f′(0),利用乘法运算律整理后,将求出的a1a2012,a2a2011,…,a1006a1007的值代入,利用同底数幂的运算法则化简后,得出f′(0)的值,即为函数在(0,f(0))处的斜率,进而确定出函数f(x) 在点(0,f(0))处的切线方程.
解答:
解:∵等比数列{an}中,a1=1,a2012=4,
∴a1a2012=a2a2011=…=a1006a1007=4=22,
∵f(x)=x(x-a1)(x-a2)…(x-a2012),
∴f′(0)=(-a1)•(-a2)•…•(-a2012)=a1•a2•…•a2012
=(a1a2012)•(a2a2011)•…•(a1006a1007)
=22•22•…•22(1006个22相乘)=21006×2=22012,
∴函数f(x) 在点(0,f(0))处的切线方程y-f(0)=22012(x-0),即y=22012x.
故答案为:y=22012x.
点评:本题考查了等比数列的性质,求导法则,利用导数研究曲线上某点的切线方程,以及直线的点斜式方程,其中利用等比数列的性质及求导法则求出f′(0)的值及切线方程的斜率是解本题的关键.



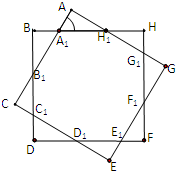 如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设∠AA1H1=α.
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设∠AA1H1=α.