
分析 根据指数函数的性质,利用换元法转化为一元二次函数,利用一元二次不等式恒成立问题转化一元二次函数的最值进行求解即可.
解答 解:f(x)=4x+1+a•2x+b=4•(2x)2+a•2x+b,
设t=2x,∵x∈[0,1],∴t∈[1,2],
则函数等价y=4t2+a•t+b,t∈[1,2],
若于?x∈[0,1],|f(x)|≤$\frac{1}{2}$都成立,
即于?t∈[1,2],|4t2+a•t+b|≤$\frac{1}{2}$都成立,
即-$\frac{1}{2}$≤4t2+a•t+b≤$\frac{1}{2}$恒成立,
设g(t)=4t2+a•t+b,要使?a∈R,不等式恒成立,
则函数g(t)的对称轴t=$\frac{3}{2}$,即-$\frac{a}{2×4}$=$\frac{3}{2}$,即a=-12,
此时g(t)=4t2-12t+b,
则抛物线开口向上,
要使-$\frac{1}{2}$≤4t2+a•t+b≤$\frac{1}{2}$恒成立,
则函数g(t)max$≤\frac{1}{2}$,且g(t)min≥-$\frac{1}{2}$,
当t=1或2时,g(t)max=g(1)=4-12+b=b-8≤$\frac{1}{2}$,即b≤$\frac{17}{2}$,
当t=$\frac{3}{2}$时,g(t)min=g($\frac{3}{2}$)=b-9≥-$\frac{1}{2}$,即b≥$\frac{17}{2}$,
即b=$\frac{17}{2}$,
故答案为:$\frac{17}{2}$.
点评 本题主要考查不等式恒成立问题,根据指数函数的性质利用换元法转化为一元二次函数,利用一元二次函数的最值性质是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 20.7% | B. | 29.3% | C. | 58.6% | D. | 41.4% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
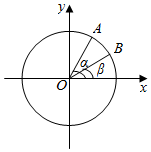 如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com