
分析 (1)x-y-1=0,可得y=x-1,代入x2=2py,可得x2-2px+2p=0,利用△=0,求出p,即可求抛物线的方程;
(2)设线段AB的中点为M(x0,y0),求出线段AB的垂直平分线的方程,直线AB的方程代入抛物线方程,利用韦达定理,进而可得S△ABC,利用换元法,构造函数,利用导数知识,即可求得结论.
解答 解:(1)由x-y-1=0,可得y=x-1,
代入x2=2py,可得x2-2px+2p=0,
∵抛物线x2=2py上点P处的切线方程为x-y-1=0,
∴△=4p2-8p=0,
∴p=2,
∴抛物线的方程x2=4y;
(2)设线段AB的中点为M(x0,y0),则x0=$\frac{{x}_{1}+{x}_{2}}{2}$,y0=2,∴kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{1}{2}$x0,
∴线段AB的垂直平分线的方程为y-2=-$\frac{2}{{x}_{0}}$(x-x0).
令x=0,得y=4,故C(0,4)为定点.
又直线AB的方程为y-2=$\frac{1}{2}$x0(x-x0),与x2=4y联立,消去y得x2-2x0x+2x02-8=0.
由韦达定理得x1+x2=2x0,x1x2=2x02-8.
直线AB的方程令x=0,得y=2-$\frac{1}{2}$x02,
∴S△ABC=$\frac{1}{2}$|2-$\frac{1}{2}$x02-4|•$\sqrt{32-4{{x}_{0}}^{2}}$=$\frac{1}{2}\sqrt{(4+{{x}_{0}}^{2})^{2}(8-{{x}_{0}}^{2})}$
令t=4+x02(12>t>4),则8-x02=12-t
设f(t)=t2(12-t)=-t3+12t2,∴f′(t)=-3t(t-8)
当4<t<8时,f′(t)>0;当12>t>8时,f′(t)<0.
∴f(t)在(4,8)上单调递增,在(8,12)上单调递减.
∴当t=8时,[f(t)]max=82×4.故△ABC面积的最大值为8.
点评 本题考查抛物线的定义,考查抛物线的标准方程,考查直线与抛物线的位置关系,考查三角形面积的计算及最值的求解,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | 1 | B. | $\frac{1}{2}$ | ||
| C. | $\frac{1}{4}$ | D. | 不是定值,与t的值相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
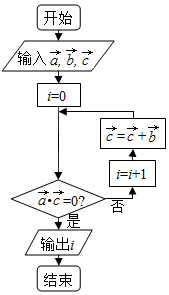 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com