
设函数f(x)=ax3+bx2+c,其中a+b=0,a,b,c均为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调区间.
科目:高中数学 来源:2015届山东省高二暑假作业二数学试卷(解析版) 题型:选择题
已知抛物线的顶点在原点,焦点在x轴的正半轴上,若抛物线的准线与双曲线5x2-y2= 20的两条渐近线围成的三角形的面积等于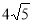 ,则抛物线的方程为
,则抛物线的方程为
A.y2=4x B.y2=8x C.x2=4y D.x2=8y
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知 ,则导函数f′(x)是( ).
,则导函数f′(x)是( ).
A.仅有最小值的奇函数
B.既有最大值,又有最小值的偶函数
C.仅有最大值的偶函数
D.既有最大值,又有最小值的奇函数
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
函数f(x)=2x﹣sinx在(﹣∞,+∞)上( ).
A.有最小值 B.是减函数 C.有最大值 D.是增函数
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:填空题
有一段“三段论”推理是这样的:“对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点;因为函数f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是函数f(x)=x3的极值点.”以上推理中(1)大前提错误;(2)小前提错误;(3)推理形式正确;(4)结论正确
你认为正确的序号为 .
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数f(x)的导函数为f′(x),满足f(x)=2xf′(2)+x3,则f′(2)等于( ).
A.﹣8 B.﹣12 C.8 D.12
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
用二分法求方程x2=2的正实根的近似解(精确度0.001)时,如果我们选取初始区间是[1.4,1.5],则要达到精确度要求至少需要计算的次数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com