
ЁОЬтФПЁПФГжжВњЦЗЕФжЪСПвдЦфжЪСПжИБъжЕКтСПЃЌВЂвРОнжЪСПжИБъжЕЛЎЗжЕШМЖШчБэЃК
жЪСПжИБъжЕm | 25ЁмmЃМ35 | 15ЁмmЃМ25Лђ35ЁмmЃМ45 | 0ЃМmЃМ15Лђ45ЁмmЃМ65 |
ЕШМЖ | вЛЕШЦЗ | ЖўЕШЦЗ | Ш§ЕШЦЗ |
ФГЦѓвЕДгЩњВњЕФетжжВњЦЗжаГщШЁ100МўВњЦЗзїЮЊбљБОЃЌМьВтЦфжЪСПжИБъжЕЃЌЕУЕНЯТЭМЕФТЪЗжВМжБЗНЭМЃЎЃЈЭЌвЛзщЪ§ОнгУИУЧјМфЕФжаЕужЕзїДњБэЃЉ
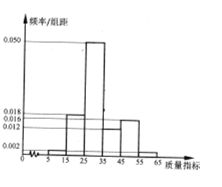
ЃЈ1ЃЉИУЦѓвЕЮЊЬсИпВњЦЗжЪСПЃЌПЊеЙСЫжЪСПЬсЩ§дТЁБЛюЖЏЃЌЛюЖЏКѓдйГщбљМьВтЃЌВњЦЗШ§ЕШЦЗЪ§YНќЫЦТњзуYЁЋHЃЈ10ЃЌ15ЃЌ100ЃЉЃЌЧыВтЫуЁАжЪСПЬсЩ§дТЁБЛюЖЏКѓетжжВњЦЗЕФЁАЖўЕШЦЗТЪЁАЃЈвЛЁЂЖўЕШЦЗЦфеМШЋВПВњЦЗАйЗжБШЃЉНЯЛюЖЏЧАЬсИпЖрЩйИіАйЗжЕуЃП
ЃЈ2ЃЉШєЦѓвЕУПМўвЛЕШЦЗЪлМл180дЊЃЌУПМўЖўЕШЦЗЪлМл150дЊЃЌУПМўШ§ЕШЦЗЪлМл120дЊЃЌвдбљБОжаЕФЦЕТЪДњЬцЯргІИХТЪЃЌЯжгавЛУћСЊПЭЫцЛњЙКТђСНМўВњЦЗЃЌЩшЦфжЇИЖЕФЗбгУЮЊXЃЈЕЅЮЛЃКдЊЃЉЃЌЧѓXЕФЗжВМСаМАЪ§бЇЦкЭћЃЎ
ЁОД№АИЁПЃЈ1ЃЉ5ИіАйЗжЕуЃЎЃЈ2ЃЉМћНтЮіЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнГщбљЕїВщЪ§ОнЃЌЧѓЕУбљБОжавЛЕШЦЗКЭЖўЕШЦЗЕФМўЪ§ЃЌЕУЕНдкбљБОжаЫљеМБШР§ЃЌдйИљОнЛюЖЏКѓВњЦЗШ§ЕШЦЗЪ§YНќЫЦТњзуYЁЋHЃЈ10ЃЌ15ЃЌ100ЃЉЕУЕНвЛЁЂЖўЕШЦЗЕФКЯИёТЪЃЌСНИіБШР§БШНЯМДПЩ.
ЃЈ2ЃЉИљОнбљЦЗЙРМЦзмЬхЃЌИУЦѓвЕЫцЛњГщШЁвЛМўВњЦЗЮЊвЛЕШЦЗЕФИХТЪЮЊ![]() ЃЌЖўЕШЦЗЕФИХТЪЮЊ
ЃЌЖўЕШЦЗЕФИХТЪЮЊ![]() ЃЌШ§ЕШЦЗЕФИХТЪЮЊ
ЃЌШ§ЕШЦЗЕФИХТЪЮЊ![]() ЃЌдйУїШЗЫцЛњБфСПXЕФЫљгаПЩФмШЁжЕЮЊ240ЃЌ270ЃЌ300ЃЌ330ЃЌ360ЃЌЗжБ№ЧѓЕУЯргІИХТЪЃЌаДГіЗжВМСадйЧѓЦкЭћ.
ЃЌдйУїШЗЫцЛњБфСПXЕФЫљгаПЩФмШЁжЕЮЊ240ЃЌ270ЃЌ300ЃЌ330ЃЌ360ЃЌЗжБ№ЧѓЕУЯргІИХТЪЃЌаДГіЗжВМСадйЧѓЦкЭћ.
ЃЈ1ЃЉИљОнГщбљЕїВщЪ§ОнжЊЃЌбљБОжавЛЕШЦЗКЭЖўЕШЦЗЙВгаЃКЃЈ0.5+0.18+0.12ЃЉЁС100ЃН80ЃЈМўЃЉ
дкбљБОжаЫљеМБШР§ЮЊ80%ЃЌ
ЛюЖЏКѓВњЦЗШ§ЕШЦЗЪ§YНќЫЦТњзуYЁЋHЃЈ10ЃЌ15ЃЌ100ЃЉЃЌ
Ыљвд100МўВњЦЗжаШ§ЕШЦЗЮЊ15МўЃЌвЛЁЂЖўЕШЦЗЪ§ЮЊ100Љ15ЃН85ЃЈМўЃЉКЯИёТЪЮЊ85%ЃЌ
ЫљвдвЛЁЂЖўЕШЦЗТЪдіМгСЫ5ИіАйЗжЕуЃЎ
ЃЈ2ЃЉгЩбљЦЗЙРМЦзмЬхжЊЃЌИУЦѓвЕЫцЛњГщШЁвЛМўВњЦЗЮЊвЛЕШЦЗЕФИХТЪЮЊ![]() ЃЌЖўЕШЦЗЕФИХТЪЮЊ
ЃЌЖўЕШЦЗЕФИХТЪЮЊ![]() ЃЌШ§ЕШЦЗЕФИХТЪЮЊ
ЃЌШ§ЕШЦЗЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
ЫцЛњБфСПXЕФЫљгаПЩФмШЁжЕЮЊ240ЃЌ270ЃЌ300ЃЌ330ЃЌ360ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
ЫљвдXЕФЗжВМСаЮЊЃК
X | 240 | 270 | 300 | 330 | 360 |
PЃЈXЃЉ |
|
|
|
|
|
XЕФЪ§бЇЦкЭћ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкМЏКЯ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЖЈвх
ЃЌЖЈвх![]() .
.
МЏКЯ![]() жаЕФдЊЫиИіЪ§МЧЮЊ
жаЕФдЊЫиИіЪ§МЧЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЃЌГЦМЏКЯ
ЃЌГЦМЏКЯ![]() ОпгааджЪ
ОпгааджЪ![]() .
.
ЃЈ1ЃЉвбжЊМЏКЯ![]() ЃЌ
ЃЌ![]() ЃЌаДГі
ЃЌаДГі![]() ЃЌ
ЃЌ![]() ЕФжЕЃЌВЂХаЖЯМЏКЯ
ЕФжЕЃЌВЂХаЖЯМЏКЯ![]() ЪЧЗёОпгааджЪ
ЪЧЗёОпгааджЪ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшМЏКЯ![]() ОпгааджЪ
ОпгааджЪ![]() ЃЌХаЖЯМЏКЯ
ЃЌХаЖЯМЏКЯ![]() жаЕФШ§ИідЊЫиЪЧЗёФмзщГЩЕШВюЪ§СаЃЌЧыЫЕУїРэгЩЃЛ
жаЕФШ§ИідЊЫиЪЧЗёФмзщГЩЕШВюЪ§СаЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЪ§Са![]() ЪЧвд
ЪЧвд![]() ЮЊЪзЯюЃЌ2ЮЊЙЋБШЕФЕШБШЪ§Са. Ъ§Са
ЮЊЪзЯюЃЌ2ЮЊЙЋБШЕФЕШБШЪ§Са. Ъ§Са![]() жаЕФЧА100ЯюЃК
жаЕФЧА100ЯюЃК![]() зщГЩЕФМЏКЯ
зщГЩЕФМЏКЯ![]() МЧзї
МЧзї![]() ЃЌНЋМЏКЯ
ЃЌНЋМЏКЯ![]() жаЕФЫљгадЊЫи
жаЕФЫљгадЊЫи![]() ДгаЁЕНДѓХХађЃЌМД
ДгаЁЕНДѓХХађЃЌМД![]() Тњзу
Тњзу![]() ЃЌЧѓ
ЃЌЧѓ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕжаЃЌвдзјБъдЕуЮЊМЋЕуЃЌвд![]() жсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЕу
жсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЕу![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЧв
ЃЌЧв![]() Й§Еу
Й§Еу![]() ЃЌЧњЯп
ЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ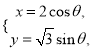 (
(![]() ЮЊВЮЪ§).
ЮЊВЮЪ§).
(Ђё)ЧѓЧњЯп![]() ЩЯЕФЕуЕНжБЯп
ЩЯЕФЕуЕНжБЯп![]() ЕФОрРыЕФзюДѓжЕЃЛ
ЕФОрРыЕФзюДѓжЕЃЛ
(Ђђ)Й§Еу![]() гыжБЯп
гыжБЯп![]() ЦНааЕФжБЯп
ЦНааЕФжБЯп![]() гыЧњЯп
гыЧњЯп ![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯжбиЖдНЧЯп
ЃЌЯжбиЖдНЧЯп![]() НЋ
НЋ![]() елЦ№ЃЌЪЙЕуAЕНДяЕуPЃЌЕуMЃЌNЗжБ№дкжБЯп
елЦ№ЃЌЪЙЕуAЕНДяЕуPЃЌЕуMЃЌNЗжБ№дкжБЯп![]() ЃЌ
ЃЌ![]() ЩЯЃЌЧвAЃЌBЃЌMЃЌNЫФЕуЙВУц.
ЩЯЃЌЧвAЃЌBЃЌMЃЌNЫФЕуЙВУц.
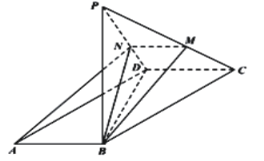
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЖўУцНЧ
ЃЌЖўУцНЧ![]() ЦНУцНЧДѓаЁЮЊ
ЦНУцНЧДѓаЁЮЊ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}Тњзу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓa1ЃЌa2ЃЌa3ЕФжЕЃЛ
ЃЈ2ЃЉЖдШЮвте§ећЪ§nЃЌanаЁЪ§ЕуКѓЕквЛЮЛЪ§зжЪЧЖрЩйЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
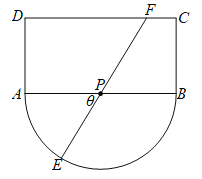
ЁОЬтФПЁПШчГЧФГЙлЙтЧјЕФЦНУцЪОвтЭМШчЭМЫљЪОЃЌЦфжаОиаЮ![]() ЕФГЄ
ЕФГЄ![]() ЧЇУзЃЌПэ
ЧЇУзЃЌПэ![]() ЧЇУзЃЌАыдВЕФдВаФ
ЧЇУзЃЌАыдВЕФдВаФ![]() ЮЊ
ЮЊ![]() жаЕу.ЮЊСЫБугкгЮПЭЙлЙтанЯаЃЌдкЙлЙтЧјЦЬЩшвЛЬѕгЩдВЛЁ
жаЕу.ЮЊСЫБугкгЮПЭЙлЙтанЯаЃЌдкЙлЙтЧјЦЬЩшвЛЬѕгЩдВЛЁ![]() ЁЂЯпЖЮ
ЁЂЯпЖЮ![]() ЁЂ
ЁЂ![]() зщГЩЕФЙлЙтЕРТЗ.ЦфжаЯпЖЮ
зщГЩЕФЙлЙтЕРТЗ.ЦфжаЯпЖЮ![]() ОЙ§дВаФ
ОЙ§дВаФ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЈВЛКЌЯпЖЮЖЫЕу
ЩЯЃЈВЛКЌЯпЖЮЖЫЕу![]() ЁЂ
ЁЂ![]() ЃЉ.вбжЊЕРТЗ
ЃЉ.вбжЊЕРТЗ![]() ЁЂ
ЁЂ![]() ЕФдьМлЮЊ
ЕФдьМлЮЊ![]() дЊУПЧЇУзЃЌЕРТЗ
дЊУПЧЇУзЃЌЕРТЗ![]() дьМлЮЊ
дьМлЮЊ![]() дЊУПЧЇУзЃЌЩш
дЊУПЧЇУзЃЌЩш![]() ЃЌЙлЙтЕРТЗЕФзмдьМлЮЊ
ЃЌЙлЙтЕРТЗЕФзмдьМлЮЊ![]() .
.
ЃЈ1ЃЉЪдЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃК
ЕФКЏЪ§ЙиЯЕЪНЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЙлЙтЕРТЗЕФзмдьМл
ЮЊКЮжЕЪБЃЌЙлЙтЕРТЗЕФзмдьМл![]() зюаЁ.
зюаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЙХДњШхМввЊЧѓбЇЩњеЦЮеСљжжЛљБОВХвеЃКРёЁЂРжЁЂЩфЁЂгљЁЂЪщЁЂЪ§ЃЌМђГЦЁАСљвеЁБ,ФГИпжабЇаЃЮЊКыбяЁАСљвеЁБЕФДЋЭГЮФЛЏЃЌЗжБ№НјааСЫжїЬтЮЊЁАРёЁЂРжЁЂЩфЁЂгљЁЂЪщЁЂЪ§ЁБСљГЁДЋЭГЮФЛЏжЊЪЖОКШќЃЌЯжгаМзЁЂввЁЂБћШ§ЮЛбЁЪжНјШыСЫЧАШ§УћЕФзюКѓНЧж№,ЙцЖЈЃКУПГЁжЊЪЖОКШќЧАШ§УћЕФЕУЗжЖМЗжБ№ЮЊ![]()
![]() Чв
Чв![]() ЃЛбЁЪжзюКѓЕУЗжЮЊИїГЁЕУЗжжЎКЭЃЌдкСљГЁБШШќКѓЃЌвбжЊМззюКѓЕУЗжЮЊ
ЃЛбЁЪжзюКѓЕУЗжЮЊИїГЁЕУЗжжЎКЭЃЌдкСљГЁБШШќКѓЃЌвбжЊМззюКѓЕУЗжЮЊ![]() ЗжЃЌввКЭБћзюКѓЕУЗжЖМЪЧ
ЗжЃЌввКЭБћзюКѓЕУЗжЖМЪЧ![]() ЗжЃЌЧвввдкЦфжавЛГЁБШШќжаЛёЕУЕквЛУћЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧ( )
ЗжЃЌЧвввдкЦфжавЛГЁБШШќжаЛёЕУЕквЛУћЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧ( )
A. ввгаЫФГЁБШШќЛёЕУЕкШ§Ућ
B. УПГЁБШШќЕквЛУћЕУЗж![]() ЮЊ
ЮЊ![]()
C. МзПЩФмгавЛГЁБШШќЛёЕУЕкЖўУћ
D. БћПЩФмгавЛГЁБШШќЛёЕУЕквЛУћ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшжБЯп![]() гыжБЯп
гыжБЯп![]() ЗжБ№гыЭждВ
ЗжБ№гыЭждВ![]()
![]() НЛгкЕу
НЛгкЕу![]() ЃЌЧвЫФБпаЮ
ЃЌЧвЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшЙ§Еу![]() ЕФЖЏжБЯп
ЕФЖЏжБЯп![]() гыЭждВ
гыЭждВ![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЪЧЗёДцдкОЙ§дЕуЃЌЧввд
СНЕуЃЌЪЧЗёДцдкОЙ§дЕуЃЌЧввд![]() ЮЊжБОЖЕФдВЃПШєгаЃЌЧыЧѓГідВЕФЗНГЬЃЌШєУЛгаЃЌЧыЫЕУїРэгЩ.
ЮЊжБОЖЕФдВЃПШєгаЃЌЧыЧѓГідВЕФЗНГЬЃЌШєУЛгаЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКx2=2pyОЙ§ЕуЃЈ2ЃЌ1ЃЉЃЎ
ЃЈЂёЃЉЧѓХзЮяЯпCЕФЗНГЬМАЦфзМЯпЗНГЬЃЛ
ЃЈЂђЃЉЩшOЮЊдЕуЃЌЙ§ХзЮяЯпCЕФНЙЕузїаБТЪВЛЮЊ0ЕФжБЯпlНЛХзЮяЯпCгкСНЕуMЃЌNЃЌжБЯпy=1ЗжБ№НЛжБЯпOMЃЌONгкЕуAКЭЕуB.ЧѓжЄЃКвдABЮЊжБОЖЕФдВОЙ§yжсЩЯЕФСНИіЖЈЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com