
| A. | $k≤-4或k≥\frac{3}{4}$ | B. | $-4≤k≤\frac{3}{4}$ | C. | $k≤-\frac{3}{4}或k≥4$ | D. | $-\frac{15}{4}≤k≤4$ |
分析 由kx+y+1-k=0,得y=-k(x-1)+1,斜率为-k,分别求出kBC,kAC,由此利用数形结合法能求出k的取值范围.
解答 解:由kx+y-k-1=0,得y=-k(x-1)+1,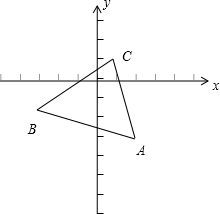
∴直线过定点C(1,1),
又A(2,-3),B(-3,-2),
讨论临界点:
当直线l经过B点(-3,-2)时,
kBC=-k=$\frac{1+2}{1+3}$=$\frac{3}{4}$,
结合图形知-k∈[$\frac{3}{4}$,+∞)成立,∴k∈(-∞,-$\frac{3}{4}$];
当直线l经过A点(2,-3)时,
kAC=-k=$\frac{1+3}{1-2}$=-4,
结合图形知-k∈(-∞,-4],∴k∈[4,+∞).
综上k∈(-∞,-$\frac{3}{4}$]∪[4,+∞).
故选:C
点评 本题考查实数的取值范围的求法,是中档题,解题时要注意直线的斜率计算公式和数形结合思想的合理运用.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
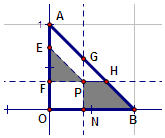 △AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.
△AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F1在以$Q(-\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
已知F1,F2为椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,F1在以$Q(-\sqrt{2},1)$为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com