
分析 求出两个函数的导函数,由导函数相等列方程,再由方程有根转化为两函数图象有交点求得a的范围
解答 解:设公切线与曲线C1切于点(x1,ax12),与曲线C2切于点(x2,${e}^{-{x}_{2}}$),
则曲线C1的导数为y′=2ax,C2的导数为y′=-e-x.
则2ax1=-${e}^{-{x}_{2}}$=$\frac{{e}^{-{x}_{2}}-a{{x}_{1}}^{2}}{{x}_{2}-{x}_{1}}$,
将${e}^{-{x}_{2}}$=-2ax1代入2ax1=$\frac{{e}^{-{x}_{2}}-a{{x}_{1}}^{2}}{{x}_{2}-{x}_{1}}$,可得2x2=x1-2,
∴a=-$\frac{{e}^{-\frac{{x}_{1}}{2}+1}}{2{x}_{1}}$,
记f(x)=-$\frac{{e}^{-\frac{x}{2}+1}}{2x}$,
则f′(x)=$\frac{{e}^{-\frac{x}{2}+1}(x+2)}{4{x}^{2}}$,当x∈(-∞,-2)时,f′(x)<0.
当x∈(-2,+∞)时,f′(x)>0,
∴当x=-2时,f(x)min=f(-2)=-$\frac{{e}^{2}}{-4}$=$\frac{{e}^{2}}{4}$.
∴a的范围是[$\frac{{e}^{2}}{4}$,+∞).
故答案为:[$\frac{{e}^{2}}{4}$,+∞)
点评 本题考查了利用导数研究过曲线上某点处的切线方程,综合考查导数的应用,综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
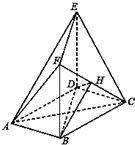 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.
如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com