
分析 (Ⅰ)求出原函数的导函数,结合f'(1)=1列式求得a值;
(Ⅱ)把(Ⅰ)中求得的a值代入函数解析式,由f(x)≤m(x-1)得到$4lnx≤m({3x-\frac{1}{x}-2})$,构造函数$g(x)=4lnx-m({3x-\frac{1}{x}-2})$,即?x∈[1,+∞),g(x)≤0.然后对m分类讨论求导求得m的取值范围;
(Ⅲ)由(Ⅱ)知,当x>1时,m=1时,$lnx≤\frac{1}{4}({3x-\frac{1}{x}-2})$成立.令$x=\frac{4i+1}{4i-3},i∈{N^*}$,然后分别取i=1,2,…,n,利用累加法即可证明结论.
解答 (Ⅰ)解:$f'(x)=\frac{{(\frac{4x+a}{x}+4lnx)(3x+1)-3(4x+a)lnx}}{{{{(3x+1)}^2}}}$--------------(1分)
由题设f'(1)=1,∴$\frac{4+a}{4}=1$,即a=0;-------------(2分)
(Ⅱ)解:$f(x)=\frac{4xlnx}{3x+1}$,?x∈[1,+∞),f(x)≤m(x-1),即$4lnx≤m({3x-\frac{1}{x}-2})$,
设$g(x)=4lnx-m({3x-\frac{1}{x}-2})$,即?x∈[1,+∞),g(x)≤0.
$g'(x)=\frac{4}{x}-m({3+\frac{1}{x^2}})=\frac{{-3m{x^2}+4x-m}}{x^2}$,g'(1)=4-4m.----------------------------(3分)
①若m≤0,g'(x)>0,g(x)≥g(1)=0,这与题设g(x)≤0矛盾;
②若m∈(0,1),当$x∈(1,\frac{{2+\sqrt{4-3{m^2}}}}{3m}),g'(x)>0$,g(x)单调递增,g(x)>g(1)=0,与题设矛盾;
③若m≥1,当x∈(1,+∞),g'(x)≤0,g(x)单调递减,g(x)≤g(1)=0,即不等式成立;
综上所述,m≥1.------------------------------------------------------------------------(7分)
(Ⅲ)证明:由(Ⅱ)知,当x>1时,m=1时,$lnx≤\frac{1}{4}({3x-\frac{1}{x}-2})$成立.---------------(9分)
不妨令$x=\frac{4i+1}{4i-3},i∈{N^*}$,
∴$ln\frac{4i+1}{4i-3}≤\frac{16i}{{({4i+1})({4i-3})}}$,
即$ln\frac{4+1}{4-3}≤\frac{16}{{({4+1})({4-3})}}$,$ln\frac{4×2+1}{4×2-3}≤\frac{16×2}{{({4×2+1})({4×2-3})}}$,$ln\frac{4×3+1}{4×3-3}≤\frac{16×3}{{({4×3+1})({4×3-3})}}$,…,$ln\frac{4n+1}{4n-3}≤\frac{16n}{{({4n+1})({4n-3})}}$.
累加可得:ln(4n+1)≤16$\sum_{i=1}^{n}$$\frac{i}{(4i+1)(4i-3)}$(n∈N*).
点评 本题主要考查导数的几何意义、导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等,是压轴题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
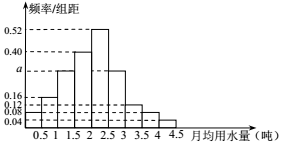 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,+∞) | B. | [$\frac{2}{3}$,1] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,3] | C. | [1,2] | D. | (2,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com