
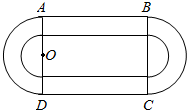
 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.分析 (1)求出塑胶跑道面积的表达式,然后求解定义域.
(2)写出运动场造价的表达式,判断函数的单调性,然后求解最小值即可.
解答 解:(1)塑胶跑道面积S=$π[{r}^{2}-({r-8)}^{2}]+\frac{10000-{πr}^{2}}{2r}×2$=$\frac{80000}{r}+8πr-64π$
∵πr2<10000,∴$8<r<\frac{100}{\sqrt{π}}$,故定义域为$(8,\frac{100}{\sqrt{π}})$.
(2)设运动场的造价为y元y=150s+30(10000-s)=120s+300000
=300000+120$(\frac{80000}{r}+8πr)-7680π$,∵$\frac{80000}{r}+8πr≥1600\sqrt{π}$,当且仅当r=$\frac{100\sqrt{π}}{π}$时取等号,
∴函数y=300000+120$(\frac{80000}{r}+8πr)-7680π$,在[30,40]上为减函数.
∴当r=40时,函数有最小值.
点评 本题考查函数的最值与应用,考查实际问题的处理策略,基本不等式的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{{4\sqrt{5}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有k个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(63,62).
把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有k个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(63,62).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
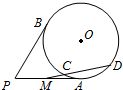 如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.
如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{13}}{13}$ | B. | $\sqrt{13}$ | C. | $\frac{\sqrt{65}}{5}$ | D. | $\sqrt{65}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com