
| A. | $\frac{\sqrt{13}}{13}$ | B. | $\sqrt{13}$ | C. | $\frac{\sqrt{65}}{5}$ | D. | $\sqrt{65}$ |
分析 根据投影的定义,应用公式向量$\overrightarrow{b}$在向量$\overrightarrow{a}$的方向上的投影|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{a}\right|}$求解.
解答 解:根据投影的定义可得:
向量$\overrightarrow{b}$在向量$\overrightarrow{a}$的方向上的投影|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{a}\right|}$=$\frac{-8+21}{\sqrt{{2}^{2}+{3}^{2}}}$=$\sqrt{13}$.
故选:B.
点评 本题主要考查向量投影的定义及求解的方法,公式与定义两者要灵活运用.解答关键在于要求熟练应用公式.


科目:高中数学 来源: 题型:解答题
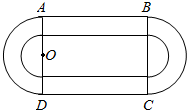 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com