
| A. | -84 | B. | -252 | C. | 252 | D. | 84 |
分析 先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.
解答 解:由题意可得${C}_{n}^{1}$=9,∴n=9,故(9x-$\frac{1}{3\sqrt{x}}$)n即(9x-$\frac{1}{3\sqrt{x}}$)9,
故(9x-$\frac{1}{3\sqrt{x}}$)9的展开式的通项公式为Tr+1=${C}_{9}^{r}$•${(-\frac{1}{3})}^{r}$•99-r•${x}^{9-\frac{3r}{2}}$,
令9-$\frac{3r}{2}$=0,求得r=6,故其展开式中的常数项为${C}_{9}^{3}$${(\frac{1}{3})}^{6}$•93=84,
故选:D.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.


科目:高中数学 来源: 题型:选择题
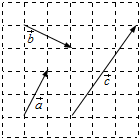 如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,(x,y∈R),则x+y=( )
如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,(x,y∈R),则x+y=( )| A. | 0 | B. | 1 | C. | 5$\sqrt{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都是奇函数 | B. | 都是偶函数 | C. | 函数f(x)的值域为R | D. | 函数g(x)的值域为R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{7}$ | B. | $24\sqrt{7}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{21}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若 的图象与
的图象与 轴围成的三角形面积大于6,求
轴围成的三角形面积大于6,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com