
分析 将坐标代入求解φ,可得函数y=sin(πx+φ)的解析式,再求解f(0)即可.
解答 解:∵函数y=sin(πx+φ)过点$({\frac{1}{6},1})$,
∴1=sin($\frac{π}{6}+$φ)
得:φ$+\frac{π}{6}$=$\frac{π}{2}+2kπ$,(k∈Z)
φ=$\frac{π}{3}+2kπ$.
那么:函数y=sin($πx+\frac{π}{3}+2kπ$),
当x=0时,可得y=sin($\frac{π}{3}+2kπ$)=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$.
故f(0)=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征和计算化简能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | {-1,0,2,3} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{9π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
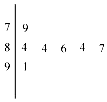 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,4 | D. | 85,1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com