练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知集合M={x|-1≤x＜3，x∈R}，N={-1，0，1，2，3}，则M∩N=（　　）
    A．{-1，0，2，3}B．{-1，0，1，2}C．{0，1，2}D．{0，1，2，3}

    分析 由M与N，求出两集合的交集即可．

    解答 解：∵M={x|-1≤x＜3，x∈R}，N={-1，0，1，2，3}，
    ∴M∩N={-1，0，1，2}，
    故选：B．

    点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知抛物线x2=2py （p＞0），其焦点F到准线的距离为1．过F作抛物线的两条弦AB和CD（点A、C在第一象限），且M，N分别是AB，CD的中点．
    （1）若AB⊥CD，求△FMN面积的最小值；
    （2）设直线AC的斜率为kAC，直线BD的斜率为kBD，且kAC+4kBD=0，求证：直线AC过定点，并求此定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．全称命题“?x∈R，x2+5x=4”的否定是（　　）
    A．$?{x_0}∈R，{x_0}^2+5{x_0}=4$B．?x∈R，x2+5x≠4
    C．$?{x_0}∈R，{x_0}^2+5{x_0}≠4$D．以上都不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知圆C：x2+y2-4x+2y-3=0和圆外一点M（4，-8）．
    （1）过M作圆C的切线，切点为D，E，圆心为C，求切线长及DE所在的直线方程；
    （2）过M作圆的割线交圆于A，B两点，若|AB|=4，求直线AB的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

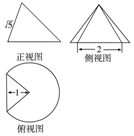    20．一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的体积为（　　）
    A．$π+\frac{2}{3}$B．$π+\frac{1}{3}$C．$\frac{3}{4}π+\frac{2}{3}$D．$\frac{3}{4}π+\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．就某地居民的月收入调查了20000人，并根据所得数据画出了样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500））．根据频率分布直方图可求得样本数据的中位数是（　　）
    A．2250B．2400C．2500D．10000

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．定义在R上的函数y=f（x）满足：f（x）+f′（x）＞1，f（0）=2017，则不等式exf（x）-ex＞2016（其中e为自然对数的底数）的解集为（　　）
    A．（2016，+∞）B．（-∞，0）∪（2016，+∞）C．（-∞，0）∪（0，+∞）D．（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若函数y=sin（πx+φ）过点$（{\frac{1}{6}，1}）$，则f（0）=$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若$sinθcosθ=\frac{1}{2}$，则$tanθ-\frac{cosθ}{sinθ}$的值是（　　）
    A．-2B．0C．±2D．$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案