
| A. | -2 | B. | 0 | C. | ±2 | D. | $\frac{1}{2}$ |
分析 由已知利用二倍角正弦求得sin2θ=1,cos2θ=0,再化切为弦,通分后求得$tanθ-\frac{cosθ}{sinθ}$的值.
解答 解:∵$sinθcosθ=\frac{1}{2}$,
∴$\frac{1}{2}sin2θ=\frac{1}{2}$,则sin2θ=1,∴cos2θ=0.
∴$tanθ-\frac{cosθ}{sinθ}$=$\frac{sinθ}{cosθ}-\frac{cosθ}{sinθ}=\frac{si{n}^{2}θ-co{s}^{2}θ}{sinθcosθ}$
=$\frac{si{n}^{2}θ-co{s}^{2}θ}{\frac{1}{2}}=-2cos2θ$=0.
故选:B.
点评 本题考查三角函数的化简求值,考查倍角公式的应用,是基础的计算题.


科目:高中数学 来源: 题型:选择题
| A. | {-1,0,2,3} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
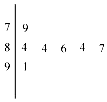 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,4 | D. | 85,1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {-2,-1} | C. | {-1} | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
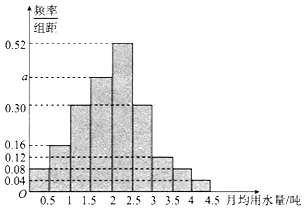 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\frac{1}{18}$ | B. | $2\frac{1}{17}$ | C. | $2\frac{2}{17}$ | D. | $2\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com