练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有垣厚五尺，两鼠对穿．大鼠日一尺，小鼠亦日一尺．大鼠日自倍，小鼠日自半．问几何日相逢？各穿几何？”，翻译成今天的话是：一只大鼠和一只小鼠分别从的墙两侧面对面打洞，已知第一天两鼠都打了一尺长的洞，以后大鼠每天打的洞长是前一天的2倍，小鼠每天打的洞长是前一天的一半，已知墙厚五尺，问两鼠几天后相见？相见时各打了几尺长的洞？设两鼠x 天后相遇（假设两鼠每天的速度是匀速的），则x=（　　）
    A．$2\frac{1}{18}$B．$2\frac{1}{17}$C．$2\frac{2}{17}$D．$2\frac{1}{9}$

    分析 由于前两天大鼠打1+2尺，小鼠打1+$\frac{1}{2}$尺，因此前两天两鼠共打3+1.5=4.5．第三天，大鼠打4尺，小鼠打$\frac{1}{4}$尺，因此第三天相遇．设第三天，大鼠打y尺，小鼠打0.5-y尺，可得$\frac{y}{4}=\frac{0.5-y}{\frac{1}{4}}$，解得y，进而得出．

    解答 解：由于前两天大鼠打1+2尺，小鼠打1+$\frac{1}{2}$尺，因此前两天两鼠共打3+1.5=4.5．
    第三天，大鼠打4尺，小鼠打$\frac{1}{4}$尺，因此第三天相遇．
    设第三天，大鼠打y尺，小鼠打0.5-y尺，
    则$\frac{y}{4}=\frac{0.5-y}{\frac{1}{4}}$，解得y=$\frac{8}{17}$．
    相见时大鼠打了1+2+$\frac{8}{17}$=$3\frac{8}{17}$尺长的洞，小鼠打了1+$\frac{1}{2}$+$\frac{1}{34}$=$1\frac{9}{17}$尺长的洞，
    x=2+$\frac{8}{17}÷4$=2$\frac{2}{17}$天，
    故选：C．

    点评 本题考查了等差数列与等比数列的通项公式性质与求和公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．若$sinθcosθ=\frac{1}{2}$，则$tanθ-\frac{cosθ}{sinθ}$的值是（　　）
    A．-2B．0C．±2D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在空间直角坐标系中，平面α内有M（m，-2，1）和N（0，m，3）两点，平面α的一个法向量为$\overrightarrow{n}$=（3，1，2），则m等于（　　）
    A．-2B．2C．3D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．直线x-y+3=0被圆x2+y2+4x-4y+6=0截得的弦长等于（　　）
    A．2$\sqrt{3}$B．$\sqrt{6}$C．$\sqrt{3}$D．$\frac{\sqrt{6}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设$α∈（\frac{π}{2}，π）$，且$sinα（sinα+cosα）=\frac{21}{25}$，则tanα的值为-7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．执行如图所示的程序框图，若输出S的值为0.99，则判断框内可填入的条件是（　　）
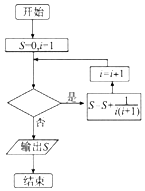
    A．i＜100B．i≤100C．i＜99D．i≤98

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知p：方程x2+2x+m=0无实数根，q：方程$\frac{{x}^{2}}{m-1}$+y2=1是焦点在x轴上的椭圆，若“非p”与“p且q”同时为假命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知定义在R上的奇函数f（x）在（0，+∞）上单调递增，f（1）=0，若f（x-2）≥0，则x的取值范围是（　　）
    A．[1，3]B．[1，2]∪[2，3]C．[1，2]∪[3，+∞]D．[-∞，1]∪[3，+∞]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=$\frac{a（x-1）}{{x}^{2}}$，其中a＞0．
    （1）求函数f（x）的单调区间；
    （2）设g（x）=xlnx-x2f（x），求g（x）在区间[1，e]上的最小值（其中e为自然对数的底数）

    查看答案和解析>>

    同步练习册答案