
分析 (1)求导数,利用导数求函数的单调性区间;
(2)利用导数求函数g(x)在闭区间上的最小值.
解答 解:(1)f′(x)=$\frac{a({-x}^{2}+2x)}{{x}^{4}}$,(x≠0),
因为a>0,所以由f′(x)>0,-x2+2x>0得0<x<2,此时函数单调递增.
由f′(x)<0,得-x2+2x<0,即x>2或x<0,此时函数单调递减.
所以函数f(x)的单调递减区间为(-∞,0)和(2,+∞),单调递增区间为(0,2).
(2)g(x)=xlnx-x2f(x)=xlnx-a(x-1),
则g'(x)=lnx+1-a,由g'(x)=lnx+1-a=0,解得x=ea-1.
所以在区间(0,ea-1)上,函数单调递减,在(ea-1.,+∞)上,函数单调递增.
①当ea-1.≤1,即0<a≤1时,在区间[l,e]上g(x)单调递增,所以g(x)的最小值为g(1)=0.
②当ea-1.≥e,即a≥2时,在区间[l,e]上g(x)单调递减,所以g(x)的最小值为g(e)=e+a-ae.
③当1<ea-1.<e,即1<a<2时,g(x)的最小值为g(ea-1)=(a-1)ea-1-a(ea-1-1)=a-ea-1.
综上当0<a≤1时,g(x)的最小值为g(1)=0.
当1<a<2时,g(x)的最小值为g(ea-1),
当≥2时,g(x)的最小值为g(e)=e+a-ae.
点评 本题主要考查利用导数研究函数的最值和函数的单调区间,比较综合.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | $2\frac{1}{18}$ | B. | $2\frac{1}{17}$ | C. | $2\frac{2}{17}$ | D. | $2\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
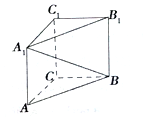 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 双曲线 | C. | 椭圆 | D. | 两条射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.
已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com