
分析 用数学归纳法证明:(1)当n=1时,去证明等式成立;(2)假设当n=k时,等时成立,用上归纳假设后,去证明当n=k+1时,等式也成立即可.
解答 证明:(1)当n=1时,左边=1,右边=21-1=1,
∴等式成立…2分
(2)假设当n=k时,等时成立,即1+2+22+…+2k-1=2k-1…4分
那么,当n=k+1时,1+2+22+…+2k-1+2k=2k-1+2k…6分
=2×2k-1
=2k+1-1…8分
这就是说,当n=k+1时,等式也成立…9分
根据(1)和(2),可知对n∈N*等式成立…10分
点评 本题考查数学归纳法,用好归纳假设是关键,考查逻辑推理与证明的能力,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{∧}{y}$=x+1 | B. | $\stackrel{∧}{y}$=0.7x+1.5 | C. | $\stackrel{∧}{y}$=2 x+1 | D. | $\stackrel{∧}{y}$=x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
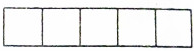 有一个经验级别达到25级的QQ好友,准备将自己QQ农场的15块空地连在一起的5块(如图)种上种植级别分别为22级、23级、25级的樱桃、荔枝和杨桃三种果树种子,如果同一种果树种子必须种在相邻的地中,则不同的种法有36种.
有一个经验级别达到25级的QQ好友,准备将自己QQ农场的15块空地连在一起的5块(如图)种上种植级别分别为22级、23级、25级的樱桃、荔枝和杨桃三种果树种子,如果同一种果树种子必须种在相邻的地中,则不同的种法有36种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{400π}{3}cm$ | B. | $\frac{20π}{3}cm$ | C. | $\frac{200π}{3}cm$ | D. | $\frac{40π}{3}cm$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lnx2与g(x)=2lnx是同一个函数 | B. | $cos\frac{π}{12}=\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | ||
| C. | △ABC中,$cos(A+B)+sin\frac{C}{2}$的最小值是-1 | D. | 因为$\sqrt{2}=2cos\frac{π}{4}$,所以$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com