
| A. | f(x)=lnx2与g(x)=2lnx是同一个函数 | B. | $cos\frac{π}{12}=\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | ||
| C. | △ABC中,$cos(A+B)+sin\frac{C}{2}$的最小值是-1 | D. | 因为$\sqrt{2}=2cos\frac{π}{4}$,所以$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$ |
分析 根据函数相等的定义,可判断A;利用半角公式求出$cos\frac{π}{12}$,可判断B;求出$cos(A+B)+sin\frac{C}{2}$的最小值,可判断C;利用半角公式判断$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$是否成立,可判断D
解答 解:A中,f(x)=lnx2的定义域为{x|x≠0},而g(x)=2lnx的定义域为{x|x>0},故不是同一个函数,故A错误;
$cos\frac{π}{12}$=$\sqrt{\frac{1+cos\frac{π}{6}}{2}}$=$\sqrt{\frac{1+\frac{\sqrt{3}}{2}}{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,故B错误;
△ABC中,$cos(A+B)+sin\frac{C}{2}$=-cosC$+sin\frac{C}{2}$=$2si{n}^{2}\frac{C}{2}+sin\frac{C}{2}-1$=$2(sin\frac{C}{2}+\frac{1}{4})^{2}-\frac{9}{8}$的最小值为$\frac{9}{8}$,故C错误;
因为$\sqrt{2}=2cos\frac{π}{4}$,所以$\sqrt{2+\sqrt{2}}$=$\sqrt{2+2cos\frac{π}{4}}$=$\sqrt{2+2(2co{s}^{2}\frac{π}{8}-1)}$=$\sqrt{4co{s}^{2}\frac{π}{8}}$=|$2cos\frac{π}{8}$|=$2cos\frac{π}{8}$,故D正确;
故选:D.
点评 本题以命题的真假判断为载体,考查了半角公式,函数相等的定义,三角函数的最值等知识点,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
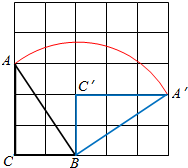 如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.
如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com