
分析 (1)由题意得|x2-1|=a|x-1|,从而可得a<0;
(2)化简h(x)=|f(x)|+g(x)-a2=|x2-1|+a|x-1|-a2=$\left\{\begin{array}{l}{{x}^{2}+ax-{a}^{2}-a-1,1≤x≤2}\\{-{x}^{2}-ax-{a}^{2}+a+1,-1<x<1}\\{{x}^{2}-ax-{a}^{2}+a-1,-2≤x<-1}\end{array}\right.$;从而分段讨论函数的最值,化恒成立问题为最值问题即可.
解答 解:(1)∵|x2-1|=a|x-1|,
∴|x-1|=0或|x+1|=a,
∴当a<0时,只有一实数解;
(2)h(x)=|f(x)|+g(x)-a2
=|x2-1|+a|x-1|-a2
=$\left\{\begin{array}{l}{{x}^{2}+ax-{a}^{2}-a-1,1≤x≤2}\\{-{x}^{2}-ax-{a}^{2}+a+1,-1<x<1}\\{{x}^{2}-ax-{a}^{2}+a-1,-2≤x<-1}\end{array}\right.$;
①∵$h{\;}_1(x)={x^2}+ax-{a^2}-a-1≤0$在[1,2]恒成立,
∴$\left\{\begin{array}{l}{{h}_{1}(1)≤0}\\{{h}_{1}(2)≤0}\end{array}\right.$,
∴a≥$\frac{1+\sqrt{13}}{2}$或$a≤\frac{{1-\sqrt{13}}}{2}$;
②-x2-ax-a2+a+1≤0恒成立,
即x2+ax+a2-a-1≥0;
即${h_2}(x)={x^2}+ax+{a^2}-a-1≥0$在(-1,1)恒成立,
(i)$\left\{\begin{array}{l}{-\frac{a}{2}≥1}\\{{h}_{2}(1)≥0}\end{array}\right.$,∴a≤-2;
(ii)$\left\{\begin{array}{l}{-\frac{a}{2}≤-1}\\{{h}_{2}(-1)≥0}\end{array}\right.$,∴a≥2;
(iii)$\left\{\begin{array}{l}{-1<-\frac{a}{2}<1}\\{{h}_{2}(-\frac{a}{2})≥0}\end{array}\right.$,∴-2<a≤-$\frac{2}{3}$;
综上所述,
a≥2或a≤-$\frac{2}{3}$;
(3)∵${h_3}(x)={x^2}-ax-{a^2}+a-1≤0$在[-2,-1]恒成立,
∴$\left\{\begin{array}{l}{{h}_{3}(-2)≤0}\\{{h}_{3}(-1)≤0}\end{array}\right.$,
∴a≥$\frac{3+\sqrt{21}}{2}$或$a≤\frac{{3-\sqrt{21}}}{2}$;
综上所述,a≥$\frac{3+\sqrt{21}}{2}$或$a≤\frac{{1-\sqrt{13}}}{2}$.
点评 本题考查了函数的性质的应用及分段函数的应用,同时考查了恒成立问题与最值问题的应用,属于中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
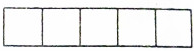 有一个经验级别达到25级的QQ好友,准备将自己QQ农场的15块空地连在一起的5块(如图)种上种植级别分别为22级、23级、25级的樱桃、荔枝和杨桃三种果树种子,如果同一种果树种子必须种在相邻的地中,则不同的种法有36种.
有一个经验级别达到25级的QQ好友,准备将自己QQ农场的15块空地连在一起的5块(如图)种上种植级别分别为22级、23级、25级的樱桃、荔枝和杨桃三种果树种子,如果同一种果树种子必须种在相邻的地中,则不同的种法有36种.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
| 年份序号x | 1 | 2 | 3 | 4 | 5 |
| 每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lnx2与g(x)=2lnx是同一个函数 | B. | $cos\frac{π}{12}=\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | ||
| C. | △ABC中,$cos(A+B)+sin\frac{C}{2}$的最小值是-1 | D. | 因为$\sqrt{2}=2cos\frac{π}{4}$,所以$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com