
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量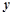 (件)与销售单价
(件)与销售单价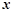 (元/件)可近似看作一次函数
(元/件)可近似看作一次函数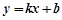 的关系(如图所示).
的关系(如图所示). 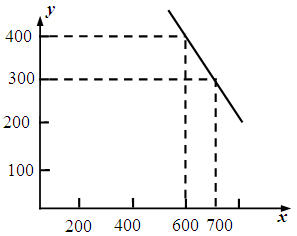
(1)根据图象,求一次函数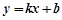 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价—成本总价)为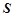 元. 试用销售单价
元. 试用销售单价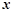 表示毛利润
表示毛利润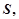 并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
科目:高中数学 来源: 题型:解答题
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: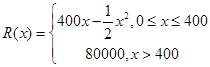 ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(注:总收益=总成本+利润)
(1)将利润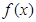 表示为月产量
表示为月产量 的函数;
的函数;
(2)当月产量 为何值时,公司所获利润最大?最大利润为多少元?
为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某兴趣小组要测量电视塔AE的高度H(单位:m).如示意图,垂直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β.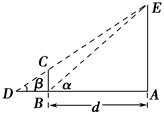
(1)该小组已测得一组α,β的值,算出了tan α=1.24,tan β=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125 m,试问d为多少时,α-β最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)= ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n同时满足下列条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m、n的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤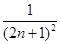 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|< .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市对排污水进行综合治理,征收污水处理费,系统对各厂一个月内排出的污水量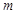 吨收取的污水处理费
吨收取的污水处理费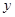 元,运行程序如下所示:请写出y与m的函数关系,并求排放污水150吨的污水处理费用.
元,运行程序如下所示:请写出y与m的函数关系,并求排放污水150吨的污水处理费用.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点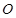 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点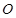 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为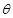 (弧度).
(弧度).
(1)求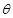 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com