
【题目】已知椭圆![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆相交另一点
与椭圆相交另一点![]() ,若
,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某消费者协会在3月15号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的1000名群众中随机抽取n名群众,按他们的年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中第1组
,其中第1组![]() 有6人,得到的频率分布直方图如图所示.
有6人,得到的频率分布直方图如图所示.
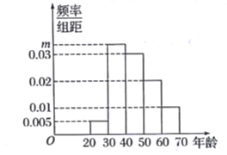
(1)求m,n的值,并估计抽取的n名群众中年龄在![]() 的人数;
的人数;
(2)已知第1组群众中男性有2人,组织方要从第1组中随机抽取3名群众组成维权志愿者服务队,求至少有两名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
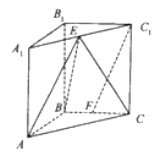
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+![]() )+cos(2x﹣
)+cos(2x﹣![]() )+cos2x﹣sin2x,x∈R.
)+cos2x﹣sin2x,x∈R.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求函数f(x)在区间[﹣![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①回归分析中,相关指数![]() 的值越大,说明残差平方和越大;
的值越大,说明残差平方和越大;
②对于相关系数![]() ,
,![]() 越接近1,相关程度越大,
越接近1,相关程度越大,![]() 越接近0,相关程度越小;
越接近0,相关程度越小;
③有一组样本数据![]() 得到的回归直线方程为
得到的回归直线方程为![]() ,那么直线
,那么直线![]() 必经过点
必经过点![]() ;
;
④![]() 是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合;
是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合;
以上几种说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次演唱会上共10 名演员(每名演员都会唱歌或跳舞),其中7人能唱歌,6人会跳舞.
(1)问既能唱歌又会跳舞的有几人?
(2)现要选出一个2人唱歌2人伴舞的节目,有多少种选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
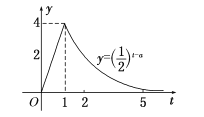
(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com