
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
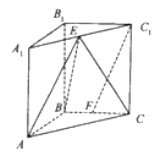
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图所示,取AB的中点M,连接MF,利用三角形中位线定理及其培训说不定判定定理可得四边形MFC1E是平行四边形,于是C1F∥EM,再利用线面平行的判定定理即可判断出结论;
(2)由直三棱柱ABC﹣A1B1C1,可得BB1⊥底面ABC,BB1⊥AB,再利用线面垂直的判定定理面面垂直的判定定理即可证明结论;
(3)由(2)可知:AB⊥BC.可建立如图所示的空间直角坐标系.求出平面ABE和平面CBE的法向量,代入公式,即可得到结果.
(1)证明:如图所示,取AB的中点M,连接MF,
则MF![]() AC,又EC1
AC,又EC1![]() AC,
AC,
∴EC1![]() MF,
MF,
∴四边形MFC1E是平行四边形,
∴C1F∥EM,又C1F平面ABE;
EM平面ABE;
∴C1F∥平面ABE.
(2)证明:由直三棱柱ABC﹣A1B1C1,∴BB1⊥底面ABC,
∴BB1⊥AB,又C1F⊥AB,BB1与C1F相交,
∴AB⊥平面ABE,又AB平面ABE,
∴平面ABE⊥平面B1BCC1;
(3)解:由(2)可知:AB⊥BC.
因此可建立如图所示的空间直角坐标系.F(0,1,0),设C1(0,2,t)(t>0),![]() (0,1,t).
(0,1,t).
由题意可取平面ACC1A1的法向量为![]() (1,1,0).
(1,1,0).
∵直线C1F和平面ACC1A1所成角的正弦值等于![]() ,
,
∴![]() |cos
|cos![]() |
|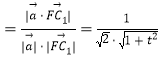 ,
,
解得t=2.
∴E(1,1,2),A(2,0,0),C(0,2,0),![]() (2,0,0),
(2,0,0),![]() (1,1,2),
(1,1,2),![]() (0,2,0).
(0,2,0).
设平面ABE的法向量为![]() (x,y,z),则
(x,y,z),则![]()
![]() 0,
0,
可得:x=0,x+y+2z=0,取y=2,可得:![]() (0,2,﹣1).
(0,2,﹣1).
同理可得平面CBE的法向量为![]() (2,0,﹣1).
(2,0,﹣1).
∴cos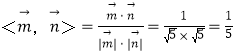 .
.
∴二面角A﹣BE﹣C的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、数学家和物理学家,他死后的墓碑上刻着一个“圆柱容球”的立体几何图形,为纪念他发现“圆柱内切球的体积是圆柱体积的![]() ,且球的表面积也是圆柱表面积的
,且球的表面积也是圆柱表面积的![]() ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为
”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为![]() ,则该圆柱的内切球体积为( )
,则该圆柱的内切球体积为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系x-O-y中,已知曲线E:![]() (t为参数)
(t为参数)
(1)在极坐标系O-x中,若A、B、C为E上按逆时针排列的三个点,△ABC为正三角形,其中A点的极角θ=![]() ,求B、C两点的极坐标;
,求B、C两点的极坐标;
(2)在直角坐标系x-O-y中,已知动点P,Q都在曲线E上,对应参数分别为t=α与t=2α (0<α<2π),M为PQ的中点,求 |MO| 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬传统文化,某市举办了“高中生诗词大赛”,现从全市参加比赛的学生中随机抽取![]() 人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为
人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() .
.
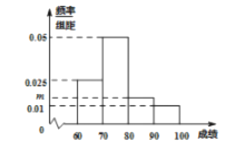
(1)求频率分布直方图中![]() 的值;
的值;
(2)在所抽取的![]() 名学生中,用分层抽样的方法在成绩为
名学生中,用分层抽样的方法在成绩为![]() 的学生中抽取了一个容量为
的学生中抽取了一个容量为![]() 的样本,再从该样本中任意抽取
的样本,再从该样本中任意抽取![]() 人,求
人,求![]() 人的成绩均在区间
人的成绩均在区间![]() 内的概率;
内的概率;
(3)若该市有![]() 名高中生参赛,根据此次统计结果,试估算成绩在区间
名高中生参赛,根据此次统计结果,试估算成绩在区间![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于其定义域
满足:对于其定义域![]() 内的任何一个自变量
内的任何一个自变量![]() ,都有函数值
,都有函数值![]() ,则称函数
,则称函数![]() 在
在![]() 上封闭.
上封闭.
(1)若下列函数:![]() ,
,![]() 的定义域为
的定义域为![]() ,试判断其中哪些在
,试判断其中哪些在![]() 上封闭,并说明理由.
上封闭,并说明理由.
(2)若函数![]() 的定义域为
的定义域为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 在其定义域
在其定义域![]() 上封闭?若存在,求出所有
上封闭?若存在,求出所有![]() 的值,并给出证明;若不存在,请说明理由.
的值,并给出证明;若不存在,请说明理由.
(3)已知函数![]() 在其定义域
在其定义域![]() 上封闭,且单调递增,若
上封闭,且单调递增,若![]() 且
且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
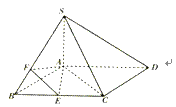
【题目】如图所示,四棱锥S﹣ABCD中,四边形ABCD为平行四边形,BA⊥AC,SA⊥AD,SC⊥CD.
(Ⅰ)求证:AC⊥SB;
(Ⅱ)若AB=AC=SA=3,E为线段BC的中点,F为线段SB上靠近B的三等分点,求直线SC与平面AEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,椭圆上动点P到一个焦点的距离的最小值为3(
,椭圆上动点P到一个焦点的距离的最小值为3(![]() -1).
-1).
(1) 求椭圆C的标准方程;
(2) 已知过点M(0,-1)的动直线l与椭圆C交于A,B两点,试判断以线段AB为直径的圆是否恒过定点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com