
分析 由已知可得an=bn-1,结合数列{bn}有连续四项在集合{-53,-23,19,37,82}中,可得等比数列{an}的四项,从而求得公比.
解答 解:由bn=an+1,得an=bn-1,
∵数列{bn}有连续四项在集合{-53,-23,19,37,82}中,
∴四项应为:-23,37,-53,82,
对应的数列{an}的四项为-24,36,-54,81,或81,-54,36,-24.
∴q=-$\frac{3}{2}$或-$\frac{2}{3}$.
故答案为:-$\frac{3}{2}$或-$\frac{2}{3}$.
点评 本题考查等比数列的通项公式,训练了由等比数列的项求公比,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (∁RA)∩B=∅ | B. | (∁RA)∩B=∁RA | C. | (∁RA)∩B=[1,2] | D. | (∁RA)∪B=R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
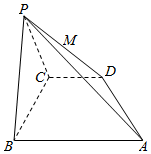 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com