
 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=2,AA1=6.若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )| A. | -$\frac{\sqrt{65}}{13}$ | B. | $\frac{\sqrt{65}}{13}$ | C. | -$\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{2}}{10}$ |
分析 由题意画出图形,建立适当的空间直角坐标系,利用空间向量所成角的余弦值求得异面直线A1E与AF所成角的余弦值.
解答 解:如图,取AB中点O,以O为原点,分别以OC,OA所在直线为x,y轴建立空间直角坐标系,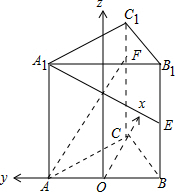
∵AB=2,AA1=6,BE=B1E,C1F=$\frac{1}{3}$CC1,
∴A(0,1,0),F($\sqrt{3}$,0,4),A1(0,1,6),E(0,-1,3),
∴$\overrightarrow{AF}=(\sqrt{3},-1,4)$,$\overrightarrow{{A}_{1}E}=(0,-2,-3)$,
∴cos<$\overrightarrow{AF},\overrightarrow{{A}_{1}E}$>=$\frac{\overrightarrow{AF}•\overrightarrow{{A}_{1}E}}{|\overrightarrow{AF}||\overrightarrow{{A}_{1}E}|}$=$\frac{2-12}{\sqrt{20}×\sqrt{13}}=-\frac{\sqrt{65}}{13}$.
∴异面直线A1E与AF所成角的余弦值为$\frac{\sqrt{65}}{13}$.
故选:B.
点评 本题考查异面直线所成角,考查空间想象能力和思维能力,训练了利用空间向量求异面直线所成角,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 30° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{35}}}{18}$ | B. | $\frac{{\sqrt{35}}}{18}$ | C. | $\frac{17}{18}$ | D. | $-\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
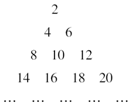 把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).
把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | $\frac{71}{5}$ | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com