
分析 利用函数关系式求解$\underset{lim}{{x}^{-}→0}$(xsin$\frac{1}{x}+a$)=f(0)=2,$\underset{lim}{x→0}$=$\frac{sin\frac{1}{x}}{\frac{1}{x}}$=0,得出a,再求解b即可.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{e}^{x}+1\\;-1<x≤0}\\{xsin\frac{1}{x}+a\\;0<x<1}\\{2x+b\\;1≤x<2}\end{array}\right.$在点x=0,x=1处的极限是存在,
∴$\underset{lim}{{x}^{-}→0}$(xsin$\frac{1}{x}+a$)=f(0)=2,
∵$\underset{lim}{x→0}$=$\frac{sin\frac{1}{x}}{\frac{1}{x}}$=0,
∴a=2,
∵f(1)=2+b,$\underset{lim}{{x}^{+}→1}$=sin1+2=f(1)=2+b,
∴b=sin1.
点评 本题简单的考察了极限的概念,运算,理解左极限,右极限的概念,属于容易题.


科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{π}{3}$ | x2 | $\frac{7π}{3}$ | x3 |
| y | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
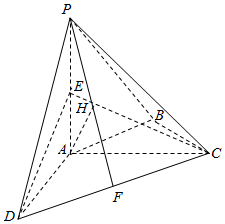 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
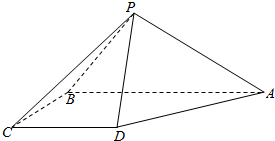 如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.
如图,四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD为直角梯形,AB=2CD=2BC=2,AB∥CD,AB⊥BC,△PAB为等腰直角三角形且PA⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com