解答:
解:(Ⅰ)∵f′(x)=
-a-
=
,
令h(x)=ax
2-x+1-a(x>0)
(1)当a=0时,h(x)=-x+1(x>0),
当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞),h(x)<0,f′(x)>0,函数f(x)单调递增.
(2)当a≠0时,由f′(x)=0,即ax
2-x+1-a=0,解得:x
1=1,x
2=
-1.
当a=
时x
1=x
2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;
当0<a<
时,
-1>1>0,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;
x∈(1,
-1)时,h(x)<0,f′(x)>0,函数f(x)单调递增;
x∈(
-1,+∞)时,h(x)>0,f′(x)<0,函数f(x)单调递减.
当a<0时,
-1<0,当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞),h(x)<0,f′(x)>0,函数f(x)单调递增.
综上所述:当a≤0时,函数f(x)在(0,1)单调递减,(1,+∞)单调递增;
当a=
时x
1=x
2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;
当0<a<
时,函数f(x)在(0,1)单调递减,(1,
-1)单调递增,(
-1,+∞)单调递减.
(Ⅱ)当a=
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x
1∈(0,2),
有f(x
1)≥f(1)=-
,
又已知存在x
2∈[1,2],使f(x
1)≥g(x
2),所以-
≥g(x
2),x
2∈[1,2],
又g(x)=(x-1)
2+b-1,x
2∈[1,2]时:g(x)是增函数,
∴g(x)max=g(2)=b,
∴b≤-
.
∴实数b取值范围是:(-∞,-
].



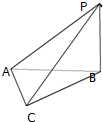 如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.
如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.