练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
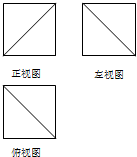
    13．一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为$\frac{1}{5}$．

    分析 由三视图得，在正方体ABCD-A1B1C1D1中，截去四面体A-A1B1D1，利用体积公式求值．

    解答 解：由三视图得，在正方体ABCD-A1B1C1D1中，截去四面体A-A1B1D1，如图所示，设正方体棱长为a，则${V_{A-{A_1}{B_1}{D_1}}}=\frac{1}{3}×\frac{1}{2}{a^3}=\frac{1}{6}{a^3}$，
    故剩余几何体体积为${a^3}-\frac{1}{6}{a^3}=\frac{5}{6}{a^3}$，所以截去部分体积与剩余部分体积的比值为$\frac{1}{5}$．
    故答案为：$\frac{1}{5}$．

    点评 本题考查了几何体的三视图求几何体的体积；关键是正确还有几何体，利用体积公式解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=4x2+kx-1在区间[1，2]上是单调函数，则实数k的取值范围是（　　）
    A．（-∞，-16]∪[-8，+∞）B．[-16，-8]C．（-∞，-8）∪[-4，+∞）D．[-8，-4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若复数$\frac{a+i}{1-i}$是纯虚数，其中i为虚数单位，则实数a的值为（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．在△ABC中，a，b，c分别是角A，B，C的对边，若tanA=3，cosC=$\frac{\sqrt{5}}{5}$，c=4．
    （1）求角B；
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知f（x）=$\frac{{2}^{x}+1}{{2}^{x+1}-a}$是奇函数．
    （1）求a的值；
    （2）判断并证明f（x）在（0，+∞）上的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列说法中，正确的是（　　）
    A．第二象限的角是钝角B．第三象限的角必大于第二象限的角
    C．方程$sinx-cosx=\frac{1}{2}$无解D．方程sinx+cosx=2无解

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=x-aex（a∈R，e为自然对数的底数）．
    （1）讨论函数f（x）的单调性；
    （2）若函数f（x）有两个零点x1，x2，求证：x1+x2＞2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．角α的终边落在区间（-3π，-$\frac{5}{2}$π）内，则角α所在象限是第三象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=|x-1|，g（x）=-|x+3|+a（a∈R）
    （1）若a=6，解不等式f（x）＞g（x）；
    （2）若函数y=2f（x）的图象恒在函数y=g（x）的图象的上方，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案