
分析 (Ⅰ)将m=-1,n=3代入f(x),求出f(x)的导数,得到函数的单调区间;
(Ⅱ)求出f(x)的导数,通过讨论m的范围判断函数的极大值的情况,进而判断出m的范围;
(Ⅲ)先求出f(x)max=f(2)=2ln2+2m-2,通过讨论m的范围去掉函数的零点问题.
解答 解:(Ⅰ)由m=-1,n=3,得:f(x)=2lnx+$\frac{1}{2}$x2-3x,(x>0),
f′(x)=$\frac{(x-1)(x-2)}{x}$,(x>0),
∴x>2或0<x<1时,f′(x)>0,1<x<2时,f′(x)<0,
∴f(x)在(0,1),(2,+∞)递增,在(1,2)递减;
(Ⅱ)f′(x)=$\frac{2}{x}$-mx-n,(x>0),
由已知得f′(2)=0,整理得2m+n=1,
∴f′(x)=$\frac{(x-2)(-mx-1)}{x}$,
m≥0时,-mx-1<0恒成立,
x>2时,f′(x)<0,0<x<2时,f′(x)>0,
f(x)在x=2处取得极大值,满足题意,
m<0时,令f′(x)=0,解得:x=2或x=-$\frac{1}{m}$,
要使f(x)在x=2处取得极大值,只需-$\frac{1}{m}$>2,解得:-$\frac{1}{2}$<m<0,
综上,m>-$\frac{1}{2}$时,f(x)在x=2处取得极大值;
(Ⅲ)由(Ⅱ)得m≥0时,f(x)在(0,2)递增,在(2,+∞)递减,
f(x)max=f(2)=2ln2+2m-2,
当f(2)>0即m>1-ln2时,f(x)有2个零点,
当f(2)=0即m=1-ln2时,f(x)有1个零点,
当f(2)<0即m<1-ln2时,f(x)没有零点,
当-$\frac{1}{2}$<m<0时,f(x)在(0,2),(-$\frac{1}{m}$,+∞)递增,在(2,-$\frac{1}{m}$)递减,
f(2)<0,f(x)至多1个零点,
法一:在(-$\frac{1}{m}$,+∞)取一点x=4-$\frac{2}{m}$=$\frac{4m-2}{m}$,代入f(x)得:
f(4-$\frac{2}{m}$)=2ln(4-$\frac{2}{m}$)-$\frac{1}{2}$m•$\frac{{4(2m-1)}^{2}}{{m}^{2}}$+(2m-2)•$\frac{4m-2}{m}$=2ln(4-$\frac{2}{m}$)>0,
f(x)在(-$\frac{1}{m}$,+∞)上必有1个零点,
法二:y=2lnx在(0,+∞)递增,y=-$\frac{1}{2}$mx2-(1-2m)x是开口向上的二次函数,
∴f(x)在(-$\frac{1}{m}$,+∞)上必有正值,即f(x)在(-$\frac{1}{m}$,+∞)上必有1个零点,
综上,m>1-ln2时,f(x)有2个零点,m=1-ln2或-$\frac{1}{2}$<m<0时,f(x)有1个零点,
0≤m<1-ln2时,f(x)没有零点.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数的零点问题,考查分类讨论思想,是一道综合题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4af(a+1)}{a+1}$>2$\sqrt{a}$f(2$\sqrt{a}$)>(a+1)f($\frac{4a}{a+1}$) | B. | $\frac{4af(a+1)}{a+1}$<2$\sqrt{a}$f(2$\sqrt{a}$)<(a+1)f($\frac{4a}{a+1}$) | ||
| C. | 2$\sqrt{a}$f(2$\sqrt{a}$)>$\frac{4af(a+1)}{a+1}$>(a+1)f($\frac{4a}{a+1}$) | D. | 2$\sqrt{a}$f(2$\sqrt{a}$)<$\frac{4af(a+1)}{a+1}$<(a+1)f($\frac{4a}{a+1}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
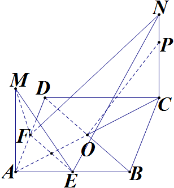 如图,正方形ABCD的边长为$2\sqrt{2}$,E、F分别为AB、AD的中点,M、N是平面ABCD同一侧的两点,MA⊥平面ABCD,MA∥NC,$MA=NC=\sqrt{3}$.
如图,正方形ABCD的边长为$2\sqrt{2}$,E、F分别为AB、AD的中点,M、N是平面ABCD同一侧的两点,MA⊥平面ABCD,MA∥NC,$MA=NC=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定小于0 | B. | 一定大于0 | C. | 等于0 | D. | 正负都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com