
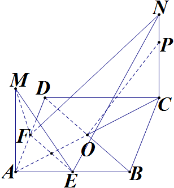
 如图,正方形ABCD的边长为$2\sqrt{2}$,E、F分别为AB、AD的中点,M、N是平面ABCD同一侧的两点,MA⊥平面ABCD,MA∥NC,$MA=NC=\sqrt{3}$.
如图,正方形ABCD的边长为$2\sqrt{2}$,E、F分别为AB、AD的中点,M、N是平面ABCD同一侧的两点,MA⊥平面ABCD,MA∥NC,$MA=NC=\sqrt{3}$.分析 (I)设AC∩EF=H,连接NH.由线面平行的性质得出OP∥NH,于是$\frac{NP}{PC}=\frac{OH}{OC}$,根据正方形的性质得出$\frac{OH}{OC}$的值;
(II)连接MH,MN,由勾股定理逆定理证明MH⊥NH,由三线合一证明MH⊥EF,故而得出MH⊥平面NEF,于是平面MEF⊥平面NEF.
解答 证明:(Ⅰ)设AC∩EF=H,连接NH.
∵OP∥平面NEF,OP?平面ACN,平面ACN∩平面NEF=NH,
∴OP∥NH,
∴NP:PC=HO:OC.
∵四边形ABCD是正方形,E,F分别为AB,AD中点,
∴HO:OC=1:2,即NP:PC=1:2.
(Ⅱ)连接MH,MN,
∵MA=NC,MA∥NC,
∴四边形ACNM是平行四边形,∴MN=AC=4.
∵MA=NC=$\sqrt{3}$,AH=$\frac{1}{4}AC$=1,CH=$\frac{3}{4}AC$=3,
∴MH=2,NH=2$\sqrt{3}$.
∴MN2=MH2+NH2,∴MH⊥NH,
又ME=MF,H是EF的中点,∴MH⊥EF,
∵EF?平面NEF,NH?平面NEF,EF∩NH=H,
∴MH⊥平面NEF,又MH?平面MEF
∴平面MEF⊥平面NEF.
点评 本题考查了线面平行的性质,面面垂直的判定,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
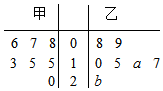 甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).
设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com