
分析 (Ⅰ)求出函数的导数,从而求出函数的单调区间;(Ⅱ)问题转化为[g(x)]min<[f(x)]max,通过讨论t结合函数的单调性分布求出[g(x)]min和[f(x)]max的值即可.
解答 解:(Ⅰ)∵函数的定义域为R,f′(x)=-$\frac{x}{{e}^{x}}$,…(1分)
∴当x<0时,f′(x)>0,当x>0时,f′(x)<0.
∴f(x)增区间为(-∞,0),减区间为(0,+∞).…(3分)
(Ⅱ)假设存在x1,x2∈[0,1],使得g(x1)<f(x2)成立,则[g(x)]min<[f(x)]max. …(5分)
由(Ⅰ)可知:[f(x)]max=f(0)=1,
∴只需[g(x)]min<1即可,…(6分)
∵g(x)=x•f(x)+t•f′(x)+e-x=$\frac{{x}^{2}+(1-t)x+1}{{e}^{x}}$,
∴g′(x)=$\frac{-{[x}^{2}-(1+t)x+t]}{{e}^{x}}$=-$\frac{(x-t)•(x-1)}{{e}^{x}}$,…(7分)
①当t≥1时,g′(x)≤0,g(x)在[0,1]上单调递减,
∴g(1)<1,即$\frac{3-t}{e}$<1,∴t>3-e,又t≥1,∴此时t的范围为[t,+∞);…(8分)
②当t≤0时,g′(x)>0,g(x)在[0,1]上单调递增,
∴g(0)<1,即1<1不可能存在; …(9分)
③当0<t<1时,在x∈[0,t],g′(x)<0,g(x)在x∈[0,t]上单调递减,
在x∈[t,1],g′(x)>0,g(x)在(t,1]上单调递增,∴g(t)<1,即$\frac{t+1}{{e}^{t}}$<1--(*)
由(Ⅰ)知,h(t)=$\frac{t+1}{{e}^{t}}$在(0,1)上单调递减,∴t∈(0,1),h(t)=$\frac{t+1}{{e}^{t}}$<h(0)=1,恒成立,
∴t∈(0,1).…(11分)
综上所述,存在t∈(0,+∞),使得命题成立. …(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道综合题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
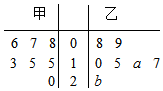 甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{3}})$ | B. | $({\sqrt{2},\sqrt{3}})$ | C. | $({\frac{1}{2},\frac{{\sqrt{3}}}{2}})$ | D. | $({\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com