练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知：等差数列{an}中，a3=5，a5=9．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若${b_n}={2^{a_n}}$，Sn是数列{bn}的前n项和，求Sn．

    分析 （Ⅰ）利用d=$\frac{{a}_{5}-{a}_{3}}{5-3}$可求出公差d=2，进而利用an=a3+（n-3）d计算即得结论；
    （Ⅱ）通过（I）可知bn=$\frac{1}{2}$•4n，进而利用等比数列的求和公式计算即得结论．

    解答 解：（Ⅰ）∵a3=5，a5=9，
    ∴d=$\frac{{a}_{5}-{a}_{3}}{5-3}$=$\frac{9-5}{5-3}$=2，
    ∴an=a3+（n-3）d=5+2（n-3）=2n-1；
    （Ⅱ）由（I）可知${b_n}={2^{a_n}}$=22n-1=$\frac{1}{2}$•4n，
    所以Sn=$\frac{1}{2}$•$\frac{4（1-{4}^{n}）}{1-4}$=$\frac{2}{3}$（4n-1）．

    点评 本题考查数列的通项及前n项和，考查运算求解能力，注意解题方法的积累，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知数列{an}的前n项和为Sn=n2，数列{bn}的前n项和为Tn=2bn-1．
    （1）求数列{an}与{bn}的通项公式；
    （2）求证：$\frac{1}{{a}_{2}+{S}_{1}}$+$\frac{1}{{a}_{3}+{S}_{2}}$+…+$\frac{1}{{a}_{n+1}+{S}_{n}}$＜$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设$\overrightarrow{e}$是与向量$\overrightarrow{AB}$共线的单位向量，$\overrightarrow{AB}$=3$\overrightarrow{e}$，又向量$\overrightarrow{BC}$=-5$\overrightarrow{e}$，若$\overrightarrow{AB}$=λ$\overrightarrow{AC}$，则λ=-$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设函数$f（x）=2ln{x^2}-\frac{1}{2}m{x^2}-nx$．
    （I）若m=-1，n=3，求函数y=f（x）的单调区间；
    （Ⅱ）若x=2是f（x）的极大值点，求出m的取值范围；
    （Ⅲ）在（Ⅱ）的条件下，试讨论y=f（x）零点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{3x}{a}$-2x2+lnx，其中a为正常数．
    （1）若a=1，求函数f（x）的单调区间；
    （2）若函数f（x）在区间[2，4]上为单调递增函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

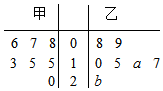    3．甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示（下面简称甲数据、乙数据），且乙数据的众数为17，甲数据的平均数比乙数据平均数少2．
    （1）求a，b的值，并计算乙数据的方差；
    （2）现从乙数据中不高于16的数据中随机抽取两个，求至少有一个数据小于10的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=lnx，$g（x）=-\frac{k}{x}，（k≠0）$
    （Ⅰ）求曲线y=f（x）在（e，f（e））处的切线方程；
    （Ⅱ）求函数h（x）=f（x）-g（x）的单调递增区间；
    （Ⅲ）若对?x∈（-∞，0）∪（0，+∞）都有f（|x|）≥g（|x|）成立，试确定实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知i是虚数单位，若复数（1+ai）（2-i）是纯虚数（a∈R），则复数a+i的共轭复数为-2-i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=1+2sin（2x-$\frac{π}{3}$）．
    （1）用五点法作图作出f（x）在x∈[0，$\frac{π}{2}$]的图象；
    （2）求f（x）在x∈[$\frac{π}{4}$，$\frac{π}{2}$]的最大值和最小值．

    查看答案和解析>>

    同步练习册答案