
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 至多只有一个公共点,求实数
至多只有一个公共点,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)利用参数方程、极坐标方程与直角坐标方程的互化公式把曲线![]() 和直线
和直线![]() 的方程化为直角坐标方程,并联立直线
的方程化为直角坐标方程,并联立直线![]() 和曲线
和曲线![]() 的直角坐标方程,得到关于
的直角坐标方程,得到关于![]() 的一元二次方程,利用判别式
的一元二次方程,利用判别式![]() 即可求出实数
即可求出实数![]() 的取值范围;
的取值范围;
![]() 根据题意,设
根据题意,设![]() ,
,![]() ,
,![]() 的中点
的中点![]() 为
为![]() ,直线
,直线![]() 和曲线
和曲线![]() 的直角坐标方程联立,得到关于
的直角坐标方程联立,得到关于![]() 的一元二次方程,由两个交点
的一元二次方程,由两个交点![]() ,
,![]() 可得判别式
可得判别式![]() ,求出
,求出![]() 取值范围,利用韦达定理和点
取值范围,利用韦达定理和点![]() 在直线
在直线![]() 上表示出点
上表示出点![]() 坐标,消去参数
坐标,消去参数![]() 即可求出
即可求出![]() ,
,![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
(1)因为曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
消去参数![]() 可得,曲线
可得,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
由题意知,直线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,
,
因为![]() ,所以直线
,所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
联立方程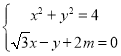 ,可得
,可得![]() ,
,
因为直线![]() 与曲线
与曲线![]() 至多只有一个公共点,
至多只有一个公共点,
所以判别式![]() ,解得
,解得![]() 或
或![]() ,
,
所以所求实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
(2)设![]() ,
,![]() ,
,![]() 的中点
的中点![]() 为
为![]() ,
,
联立方程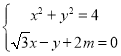 ,可得
,可得![]() ,
,
所以判别式![]() ,解得
,解得![]() ,
,
由韦达定理可得,![]() ,
,
因为点![]() 在直线
在直线![]() 上,所以
上,所以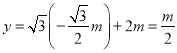 ,
,
所以可得![]() ,
,![]() 即为点
即为点![]() 的轨迹方程.
的轨迹方程.


科目:高中数学 来源: 题型:
【题目】已知椭圆G:![]() 的右焦点为F,过F的直线l交椭圆于A、B两点,直线与l不与坐标轴平行,若AB的中点为N,O为坐标原点,直线ON交直线x=3于点M.
的右焦点为F,过F的直线l交椭圆于A、B两点,直线与l不与坐标轴平行,若AB的中点为N,O为坐标原点,直线ON交直线x=3于点M.
(1)求证:MF⊥l;
(2)求![]() 的最大值,
的最大值,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且
,且![]() 所在直线的斜率之积等于
所在直线的斜率之积等于![]() ,记顶点
,记顶点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为
为![]() 的重心(
的重心(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为
为等比数列,公比为![]() .令
.令![]() .
.
(1)若![]() .
.
①当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
②设![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小?并证明你的结论.
的大小?并证明你的结论.
(2)问集合![]() 中最多有多少个元素?并证明你的结论.
中最多有多少个元素?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法正确的是( )

A.第一场得分的中位数为![]() B.第二场得分的平均数为
B.第二场得分的平均数为![]()
C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为3的正方形ABCD中,点E,F分别在边AB,BC上(如图1),且BE=BF,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′(如图2).

(1)求证:A′D⊥EF;
(2)BF![]() BC时,求点A′到平面DEF的距离.
BC时,求点A′到平面DEF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,固定边
,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 、
、![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,
取得最小值时,![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一岛礁旁有两条航道![]() 与
与![]() ,
,![]() .一日,我方船只甲在
.一日,我方船只甲在![]() 航道上巡逻,在与
航道上巡逻,在与![]() 相距50公里的点
相距50公里的点![]() 处,发现不明身份的船乙刚驶过点
处,发现不明身份的船乙刚驶过点![]() ,并沿
,并沿![]() 方向以40公里/小时的速度运动,船甲立即沿
方向以40公里/小时的速度运动,船甲立即沿![]() 方向以
方向以![]() 公里/小时(
公里/小时(![]() )的速度追击,且甲到达点
)的速度追击,且甲到达点![]() 即停止前行(乙可继续前进).设甲出发时,经过
即停止前行(乙可继续前进).设甲出发时,经过![]() 小时甲,乙之间的距离为
小时甲,乙之间的距离为![]() 公里,当
公里,当![]() 最小时,可以达到最佳的驱离距离.
最小时,可以达到最佳的驱离距离.
(1)试求![]() 的解析式,并写出定义域;
的解析式,并写出定义域;
(2)求最多经过多长时间,我船可以达到最佳的驱离距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“完美区间”,另外,定义区间
的“完美区间”,另外,定义区间![]() 的“复区间长度”为
的“复区间长度”为![]() ,已知函数
,已知函数![]() ,则( )
,则( )
A.![]() 是
是![]() 的一个“完美区间”
的一个“完美区间”
B. 是
是![]() 的一个“完美区间”
的一个“完美区间”
C.![]() 的所有“完美区间”的“复区间长度”的和为
的所有“完美区间”的“复区间长度”的和为![]()
D.![]() 的所有“完美区间”的“复区间长度”的和为
的所有“完美区间”的“复区间长度”的和为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com