
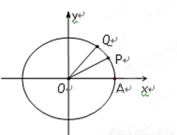
如图,设A是单位圆和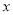 轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且
轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且 ,
,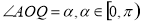 .
.
(1)若点Q的坐标是 ,求
,求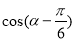 的值;
的值;
(2)设函数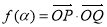 ,求
,求 的值域.
的值域.
(1)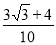 ;(2)
;(2)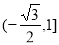 .
.
【解析】
试题分析:
解题思路:(1)利用三角函数的单位圆定义求出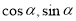 ,再利用两角差的余弦公式进行求值;(2)利用平面向量的数量积定义化简得
,再利用两角差的余弦公式进行求值;(2)利用平面向量的数量积定义化简得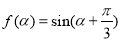 ,再结合三角函数的图像求其值域 .
,再结合三角函数的图像求其值域 .
规律总结:对于以平面向量为载体考查三角函数问题,要正确利用平面向量知识化为三角函数关系式,再利用三角函数的有关公式进行变形;涉及三角函数的周期、最值、单调性、对称性等问题,往往先根据三角函数恒等变形化为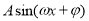 的形式,再利用三角函数的图像与性质进行求解.
的形式,再利用三角函数的图像与性质进行求解.
试题解析:(1)由已知可得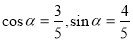 .
.
所以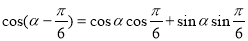
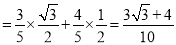 .
.
(2)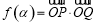
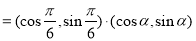
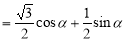
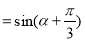 .
.
因为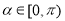 ,则
,则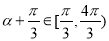 ,所以
,所以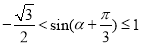 .
.
故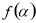 的值域是
的值域是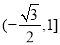 .
.
考点:1.三角函数的定义;2.两角和差的三角公式;3.平面向量的数量积;4.三角函数的图像与性质.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源:2015届福建省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
观察 ,
,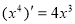 ,
,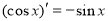 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在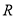 上的函数
上的函数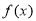 满足
满足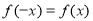 ,记
,记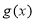 为
为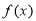 的导函数,则
的导函数,则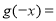 ( )
( )
A.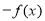 B.
B.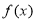 C.
C.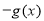 D.
D.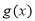
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
记集合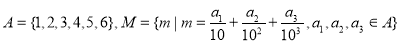 ,将M中的元素按从小到大排列,则第70个是( ).
,将M中的元素按从小到大排列,则第70个是( ).
A.0.264 B.0.265 C.0.431 D.0.432
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
观察下列关于两个变量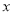 和
和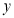 的三个散点图,它们从左到右的对应关系依次为( ).
的三个散点图,它们从左到右的对应关系依次为( ).
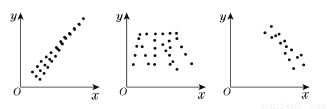
A.正相关、负相关、不相关
B.负相关、不相关、正相关
C.负相关、正相关、不相关
D.正相关、不相关、负相关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com