
| AB |
| AC |
| AB |
| AC |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3 |
|
| π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 4 |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x) |
| x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a-1 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
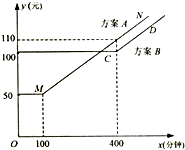 移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).
移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 2e |
| e2+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com