练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知各项均为正数的等比数列{an}中，a2=1，则其前3项的和S3的取值范围是（　　）
    A．（1，+∞）B．（0，2]C．（0，3]D．[3，+∞）

    分析 首先由等比数列的通项入手表示出S3（即q的代数式），然后利用均值不等式求出S3的范围．

    解答 解：∵等比数列{an}中，a2=1，
    ∴S3=a1+a2+a3=a2（1+q+$\frac{1}{q}$），
    ∵公比q＞0时，${S}_{3}=1+q+\frac{1}{q}$≥$1+2\sqrt{q•\frac{1}{q}}$=3．
    当且仅当q=1时上式等号成立．
    ∴前3项的和S3的取值范围是[3，+∞）．
    故选：D．

    点评 解本题考查等比数列前n项和的意义、等比数列的通项公式及均值不等式的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．Z=$\frac{2}{1+i}$，则Z的模等于$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

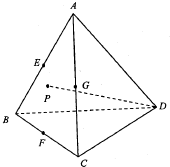    18．如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点，点P在侧面ABC及其边界上运动，DP⊥AB，则动点P的轨迹是（　　）
    A．线段FGB．线段EGC．线段EFD．线段EC

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．16个同类产品中有14个正品，2个次品，从中任意抽取3个，则下列事件中概率为1的是（　　）
    A．三个都是正品B．三个都是次品
    C．三个中至少有一个是正品D．三个中至少有一个次品

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．函数y=x3（x＞0）的图象在点（ak，ak3）处的切线所对应的一次函数的零点为ak+1，其中k∈N*．若a1=2，则a1+a3+a5的值是$\frac{266}{81}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．下列不等关系的推导中，正确的个数为（　　）
    ①a＞b，c＞d⇒ac＞bd②a＞b⇒$\frac{1}{a}$＜$\frac{1}{b}$③a＞b⇒an＞bn④$\frac{1}{x}$＞1⇒0＜x＜1．
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在一段时间内有100辆汽车经过某交通岗，有2辆汽车速度小于35km/h，有3辆汽车的速度大于75km/h，时速（单位：km/h）频率分布直方图如图所示，
    （1）求时速超过60km/h的汽车的数量；
    （2）从时速在[30，40）与[70，80]的两部分中共取两辆汽车，速度分别为v1，v2，求这两辆汽车的时速满足v1＜35，70＜v2≤75的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．数列{an}定义如下：a1=a，0≤a≤1，an+1=2（an-an2）（n∈N+）
    （1）当a=$\frac{1}{2}$时，求a4的值；
    （2）试确定实数a的值，使得a3=a4成立；
    （3）求证：当0＜a＜1且a≠$\frac{1}{2}$时，总有an+1＞an（n≥2，n∈N+）成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（　　）
    A．$\frac{11}{4}$B．$\frac{9}{4}$C．$\frac{29}{16}$D．$\frac{33}{16}$

    查看答案和解析>>

    同步练习册答案