
【题目】设![]() 、
、![]() 、
、![]() 是三条不同的直线,
是三条不同的直线,![]() 、
、![]() 、
、![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() 是两条异面直线,
是两条异面直线,![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确命题的序号是( )
A.①③B.①④C.②③D.②④
【答案】A
【解析】
根据线面平行的性质定理以及空间中平行直线的传递性可判断出命题①的正误;根据面面关系可判断出命题②的正误;利用线面平行的性质定理以及直线与平面垂直的判定定理可判断出命题③的正误;根据线面垂直的判定定理、面面垂直的判定定理可判断出命题④的正误.
对于命题①,![]() ,
,![]() ,
,![]() ,由直线与平面平行的性质定理可得
,由直线与平面平行的性质定理可得![]() ,
,
![]() ,
,![]() ,由平行线的传递性可知
,由平行线的传递性可知![]() ,命题①正确;
,命题①正确;
对于命题②,![]() ,
,![]() ,则平面
,则平面![]() 与平面
与平面![]() 平行或相交,命题②错误;
平行或相交,命题②错误;
对于命题③,过直线![]() 作平面
作平面![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,若
,若![]() ,根据平行线的传递性可得
,根据平行线的传递性可得![]() ,这与题意矛盾,
,这与题意矛盾,
又![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() 、
、![]() ,
,![]() ,
,
命题③正确;
对于命题④,![]() ,
,![]() ,
,![]() ,
,![]() ,但
,但![]() 、
、![]() 不一定垂直,则
不一定垂直,则![]() 与
与![]() 不一定垂直,所以
不一定垂直,所以![]() 与
与![]() 也不一定垂直,命题④错误.
也不一定垂直,命题④错误.
因此,正确的命题序号为①③.
故选:A.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】如图:已知某公园的四处景观分别位于等腰梯形![]() 的四个顶点处,其中
的四个顶点处,其中![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() .现拟规划在
.现拟规划在![]() (不包括端点)路段上增加一个景观
(不包括端点)路段上增加一个景观![]() ,并建造观光路直接通往
,并建造观光路直接通往![]() 处,造价为每千米
处,造价为每千米![]() 万元,又重新装饰
万元,又重新装饰![]() 路段,造价为每千米
路段,造价为每千米![]() 万元.
万元.
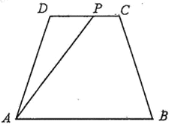
(1)若拟修建观光路![]() 路段长为
路段长为![]() 千米,求
千米,求![]() 路段的造价;
路段的造价;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,
,![]() 段的总造价最低.
段的总造价最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学小组到进行社会实践调查,了解鑫鑫桶装水经营部在为如何定价发愁。进一步调研了解到如下信息:该经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表:
销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
根据以上信息,你认为该经营部定价为多少才能获得最大利润?( )
A.每桶8.5元B.每桶9.5元C.每桶10.5元D.每桶11.5元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.
(1)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下列联表:能否据此判断有97.5%的把握认为“礼让斑马线”行为与驾龄有关?
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
(2)下图是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为的折线图:
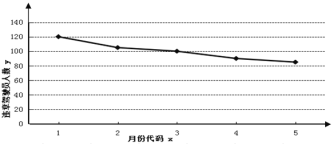
请结合图形和所给数据求违章驾驶员人数y与月份x之间的回归直线方程![]() ,并预测该路口7月份的不“礼让斑马线”违章驾驶员人数.
,并预测该路口7月份的不“礼让斑马线”违章驾驶员人数.
附注:参考数据:![]() ,
,![]() .
.
参考公式: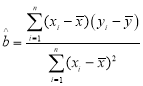 ,
,![]() ,
,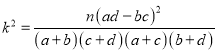 (其中
(其中![]() )
)
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com