
已知椭圆 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设 ,则
,则 等于( )
等于( )
A.  B.
B.  C.
C. D.
D. 
B
解析试题分析:解:由题意a=5,b=3,c=4,所以F点坐标为(4,0)
设直线l方程为:y=k(x﹣4),A点坐标为(x1,y1),B点坐标为(x2,y2),得P点坐标(0,﹣4k),
因为 ,所以(x1,y1+4k)=λ1(4﹣x1,﹣y1)
,所以(x1,y1+4k)=λ1(4﹣x1,﹣y1)
因为 ,所以(x2,y2+4k)=λ2(4﹣x2,﹣y2).
,所以(x2,y2+4k)=λ2(4﹣x2,﹣y2).
得λ1= ,λ2=
,λ2= .
.
直线l方程,代入椭圆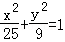 ,消去y可得(9+25k2)x2﹣200k2x+400k2﹣225=0.
,消去y可得(9+25k2)x2﹣200k2x+400k2﹣225=0.
所以x1+x2= ,x1x2=
,x1x2= .
.
所以λ1+λ2= =
= =
= =
= ,故选B.
,故选B.
考点:直线与椭圆的位置关系
点评:解决的关键是根据直线与椭圆的方程联立方程组,结合向量的坐标关系来得到,属于基础题。


科目:高中数学 来源: 题型:单选题
椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点 、
、 是它的焦点,长轴长为
是它的焦点,长轴长为 ,焦距为
,焦距为 ,静放在点
,静放在点 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点 时,小球经过的路程是( )
时,小球经过的路程是( )
A. | B. | C. | D.以上答案均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知点P是双曲线C: 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
A.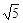 | B.2 | C. | D.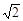 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com