
分析 (1))利用复数的运算法则与复数相等即可得出.
(2)利用共轭复数的定义、运算法则即可得出.
解答 解:(1)由已知$\frac{x}{{z}_{1}}$-$\frac{5}{{z}_{2}}$=$\frac{y}{{z}_{3}}$,得$\frac{x}{2i}$-$\frac{5}{1-3i}$=$\frac{y}{1-2i}$,----------------------(1分)
即$-\frac{1}{2}$-$\frac{x+3}{2}$i=$\frac{y}{5}$+$\frac{2y}{5}$i.-----------------------(4分)
∵x,y∈R,
∴$\left\{\begin{array}{l}\frac{y}{5}=-\frac{1}{2}\\ \frac{2y}{5}=-\frac{x+3}{2}\end{array}\right.$-----------------------(5分)
解得$\left\{\begin{array}{l}x=-1\\ y=-\frac{5}{2}\end{array}\right.$-----------------------(6分)
(2)由(1)知$\overline{{z}_{1}}$=-2i,$\overline{{z}_{2}}$=1+3i,-----------------------(8分)
则$\overline{{z}_{1}}$•$\overline{{z}_{2}}$=(-2i)(1+3i)=6-2i.-----------------------(10分)
点评 本题考查了复数的运算法则与复数相等、共轭复数的定义,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 2<b<2$\sqrt{2}$ | B. | 2≤b<2$\sqrt{2}$ | C. | 2≤b≤2$\sqrt{2}$ | D. | 2<b≤2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小说明拟合效果越好 | |
| D. | 若变量y和x之间的相关系数为r=-0.9462,则变量y和x之间具有线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | $x=-\frac{1}{2}$ | C. | x=1 | D. | $x=\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:
某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如表所示:| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 货币收入x | 40 | 42 | 44 | 47 | 50 |
| 购买商品支出y | 33 | 34 | 36 | 39 | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
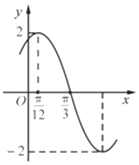 如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象.
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com