
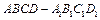 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、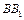 、
、 的中点.
的中点.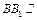 平面
平面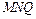 ,∴点P到平面MNQ的距离等于点B到平面MNQ的距离.设
,∴点P到平面MNQ的距离等于点B到平面MNQ的距离.设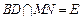 .∵平面MNQ
.∵平面MNQ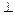 平面ABCD,∴由
平面ABCD,∴由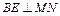 得
得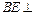 平面MNQ,∴点P到平面MNQ的距离为
平面MNQ,∴点P到平面MNQ的距离为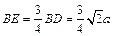 .……………5分
.……………5分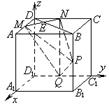
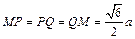 ,
,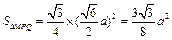 .
.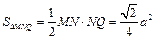 .由
.由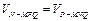 得
得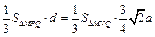 ,∴
,∴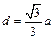 .……………10分
.……………10分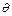 ,则
,则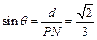 .故直线PN与平面MPQ所成的角的正弦值为
.故直线PN与平面MPQ所成的角的正弦值为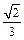 .……………12分
.……………12分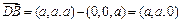 是平面MNQ的一个法向量.
是平面MNQ的一个法向量.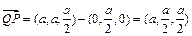 ,
,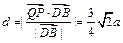 .……………5分
.……………5分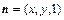 .
.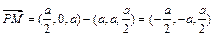 .
.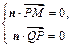 得
得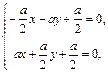 得
得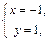
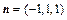 .
.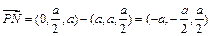 .……………10分
.……………10分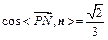 .设直线PN与平面MPQ所成的角为
.设直线PN与平面MPQ所成的角为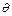 ,则
,则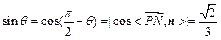 .……………12分
.……………12分

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源:不详 题型:解答题
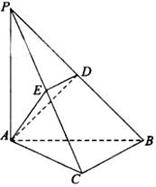
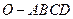 中,底面
中,底面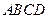 为菱形,
为菱形,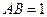 ,
,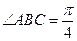 ,
,  ,
, 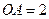 ,
,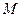 为
为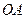 的中点,
的中点,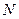 为
为 的中点
的中点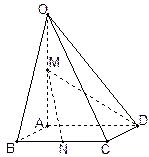
 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 a的
a的 值;
值; 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
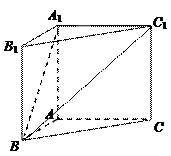
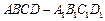 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,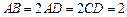 .
. C1C;
C1C;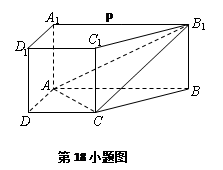
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
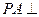 底面
底面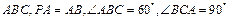 ,点
,点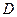 ,
,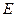 分别在棱
分别在棱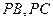 上,且
上,且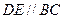 。 。
。 。 
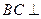 平面
平面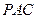 ;
;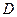 为
为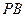 的中点时,求
的中点时,求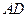 与平面
与平面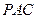 所成的角的大小;
所成的角的大小;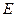 使得二面角
使得二面角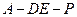 为直二面角?并说明理由.
为直二面角?并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
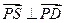 .
. 大值时,求异面直线AP与SD所成角的余弦值.
大值时,求异面直线AP与SD所成角的余弦值.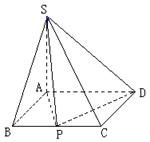
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
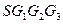 中,E、F分别是边
中,E、F分别是边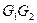 、
、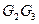 的中点,D是EF的中点,现沿SE、SF及EF把这个正方形折成一个几何体(如图乙所示),使
的中点,D是EF的中点,现沿SE、SF及EF把这个正方形折成一个几何体(如图乙所示),使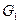 、
、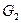 、
、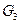 三点重合于点G,则下面结论成立的是( )
三点重合于点G,则下面结论成立的是( )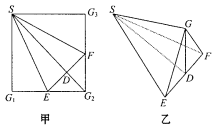
| A.SD⊥平面EFG | B.GF⊥平面SEF | C.SG⊥平面EFG | D.GD⊥平面SEF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com