
分析 (Ⅰ)根据题意P在线段F2A的中垂线上,所以|PF2|=|PA|,则|PF2|+|PF1|=|PA|+|PF1|=|AF1|=4>|F1F2|,故轨迹C是以F1,F2为焦点的椭圆,从而可求P点的轨迹C的方程;
(Ⅱ)由$\overrightarrow{OM}•\overrightarrow{ON}=-2$,得x1x2+y1y2=-2,由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+1\end{array}\right.$,得(3+4k2)x2+8kx-8=0,利用韦达定理,求直线l方程.
解答 解:(Ⅰ)因为P在线段F2A的中垂线上,所以|PF2|=|PA|,(1分)
所以|PF2|+|PF1|=|PA|+|PF1|=|AF1|=4>|F1F2|,(2分)
所以轨迹C是以F1,F2为焦点的椭圆,且$a=2,c=1,b=\sqrt{{a^2}-{c^2}}=\sqrt{3}$,(3分)
所以轨迹C的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$.(4分)
(Ⅱ)设M(x1,y1),N(x2,y2),由$\overrightarrow{OM}•\overrightarrow{ON}=-2$,得x1x2+y1y2=-2,(5分)
即x1x2+(kx1+1)(kx2+1)=-2,即(1+k2)x1x2+k(x1+x2)+3=0?(6分)
由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+1\end{array}\right.$,得(3+4k2)x2+8kx-8=0,(7分)
因为△=64k2+32(3+4k2)>0,(8分)
所以,有$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{-8k}{{3+4{k^2}}}\\{x_1}{x_2}=\frac{-8}{{3+4{k^2}}}\end{array}\right.$(9分)
代入化简得1-4k2=0,解得$k=±\frac{1}{2}$,(11分)
所以直线l方程为$y=±\frac{1}{2}x+1$.(12分)
点评 本题考查椭圆的定义与方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | -3 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3% | B. | 4% | C. | 5% | D. | 6% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
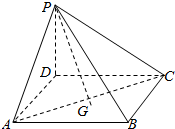 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )| A. | θ=$\frac{π}{4}$ | B. | cosθ=$\frac{2\sqrt{34}}{17}$ | C. | tanθ=$\frac{2\sqrt{2}}{3}$ | D. | sinθ=$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com