
分析 (1)由2Sn=n(n+1),利用递推关系可得:n=1时,a1=1;n≥2时,an=Sn-Sn-1,即可得出.
(2)bn=$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$,利用“裂项求和”方法即可得出:{bn}的前n项和Tn.
(3)Cn=2${\;}^{{a}_{n}}$=2n,利用等比数列的求和公式即可得出:前n项和Rn,满足Rn≥2016,转化为:2n+1-2≥2016,即可得出.
解答 解:(1)∵2Sn=n(n+1),
∴n=1时,a1=1;n≥2时,an=Sn-Sn-1=$\frac{n(n+1)}{2}$-$\frac{n(n-1)}{2}$=n,
n=1时也成立,∴an=n.
(2)bn=$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$,
∴{bn}的前n项和Tn=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=2$(1-\frac{1}{n+1})$
=$\frac{2n}{n+1}$.
(3)Cn=2${\;}^{{a}_{n}}$=2n,
∴数列{Cn}是等比数列,首项为2,公比为2,
其前n项和Rn=$\frac{2×({2}^{n}-1)}{2-1}$=2n+1-2,
满足Rn≥2016,转化为:2n+1-2≥2016,
210=1024,211=2048.
∴n+1=11,解得n=10.
∴满足Rn≥2016的最小整数n=10.
点评 本题考查了递推关系、等比数列的求和公式、“裂项求和”方法、不等式的解法、指数幂的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧.为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到统计数据如表,现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为$\frac{2}{5}$.
2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧.为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到统计数据如表,现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为$\frac{2}{5}$.| 未发病 | 发病 | 合计 | |
| 未注射疫苗 | 20 | x | A |
| 注射疫苗 | 30 | y | B |
| 合计 | 50 | 50 | 100 |
| P( K2≤K0) | 0.05 | 0.01 | 0.005 | 0.001 |
| K0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
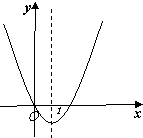 (文)二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是( )
(文)二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是( )| A. | -1≤t<3 | B. | t≥-1 | C. | 3<t<8 | D. | -1≤t<8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
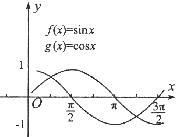 如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间$[{0,\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1.
如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间$[{0,\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com