
分析 由题意画出图形,得到要使切线段长最小,则圆心O到直线x-y+2$\sqrt{2}$=0的距离最小,由点到直线的距离公式求出O到直线的距离,再由勾股定理求得答案;求出P的坐标,当直线过原点时,直接得到直线方程,当直线不过原点时,设出直线方程的截距式x+y=a,代入点的坐标求得a值得答案.
解答 解:如图,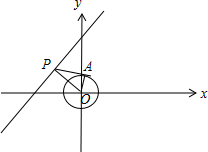
圆的半径为定值1,要使切线段长最小,则圆心O到直线x-y+2$\sqrt{2}$=0的距离最小,
由点到直线的距离公式求得O到直线的距离d=$\frac{|2\sqrt{2}|}{\sqrt{2}}=2$,
∴切线段长的最小值为$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$;
P的横坐标为$\sqrt{2}$,则P的纵坐标为3$\sqrt{2}$,即点P($\sqrt{2},3\sqrt{2}$),
当直线过原点时,直线方程为y=3x;
当直线不过原点时,设直线方程为x+y=a,则a=4$\sqrt{2}$.
此时直线方程为y=-x+4$\sqrt{2}$.
∴过点P的在两个坐标轴上的截距相等的直线方程是y=3x或y=-x+$4\sqrt{2}$.
故答案为:$\sqrt{3}$;y=3x或y=-x+4$\sqrt{2}$.
点评 本题考查直线与圆的位置关系的应用,考查了直线的截距式方程,是基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
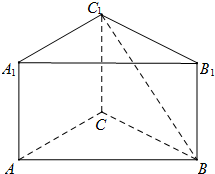 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=CC1=4
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=CC1=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,斜三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的中点.
如图所示,斜三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8] | B. | [-8,-4] | C. | (-∞,4]∪[8,+∞) | D. | (-∞,-8]∪[-4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com