
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
分析 利用向量的数乘及坐标加法运算求出$\overrightarrow{c}$的坐标,代入向量模的公式,利用配方法求得答案.
解答 解:∵$\overrightarrow{a}$=(cos25°,sin25°),$\overrightarrow{b}$=(cos70°,sin70°),
∴$\overrightarrow{c}$=$\overrightarrow{a}$+t$\overrightarrow{b}$=(cos25°+tcos70°,sin25°+tsin70°)=(cos25°+tsin20°,sin25°+tcos20°),
则|$\overrightarrow{t}$|=$\sqrt{1+{t}^{2}+2tsin45°}$=$\sqrt{{t}^{2}+\sqrt{2}t+1}=\sqrt{(t+\frac{\sqrt{2}}{2})^{2}+\frac{1}{2}}$.
∴|$\overrightarrow{c}$|的最小值为$\frac{\sqrt{2}}{2}$.
故选:A.
点评 本题考查平面向量的数量积运算,考查向量模的求法,训练了配方法求最值,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
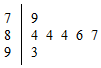 某校举行元旦汇演,七位评委为某班的小品打出的分数如茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差是$\frac{8}{5}$.
某校举行元旦汇演,七位评委为某班的小品打出的分数如茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差是$\frac{8}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com