
已知函数f(x)=ln x-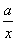 .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)<x2在(1,+∞)上恒成立,求a的取值范围.
【解】(1)由题意知f(x)的定义域为(0,+∞),且f′(x)=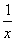 +
+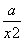 =
=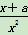 .
.
∵a>0,∴f′(x)>0,故f(x)在(0,+∞)上是单调递增函数.
(2)∵f(x)<x2,∴ln x-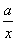 <x2.又x>0,∴a>xln x-x3.
<x2.又x>0,∴a>xln x-x3.
令g(x)=xln x-x3,h(x)=g′(x)=1+ln x-3x2,
h′(x)=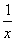 -6x=
-6x=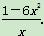
∵x∈(1,+∞)时,h′(x)<0,
∴h(x)在(1,+∞)上是减函数.∴h(x)<h(1)=-2<0,即g′(x)<0,∴g(x)在(1,+∞)上也是减函数.
g(x)<g(1)=-1,∴当a≥-1时,f(x)<x2在(1,+∞)上恒成立.
那a的取值范围是[-1,+∞).


科目:高中数学 来源: 题型:
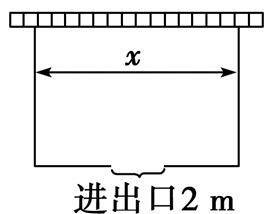
围建一个面积为368 m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口(如图所示),已知旧墙的维修费用为180元/m,新墙的造价为460元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com