
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 利用棱柱与棱锥的体积计算公式即可得出.
解答 解:三棱柱ABC-A1B1C1的体积为V,
又∵P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,
∴四棱锥B-APQC的底面积SAPQC=$\frac{1}{2}$SACC1A1
又VB-ACC1A1=${V}_{三棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$-${V}_{三棱锥B-{A}_{1}{B}_{1}{C}_{1}}$=V-$\frac{1}{3}V$=$\frac{2V}{3}$
∴VB-APQC=$\frac{1}{2}$${V}_{B-AC{C}_{1}{A}_{1}}$=$\frac{1}{2}$×$\frac{2}{3}$v=$\frac{1}{3}$${V}_{三棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$.
故选:B.
点评 本题考查了棱柱与棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
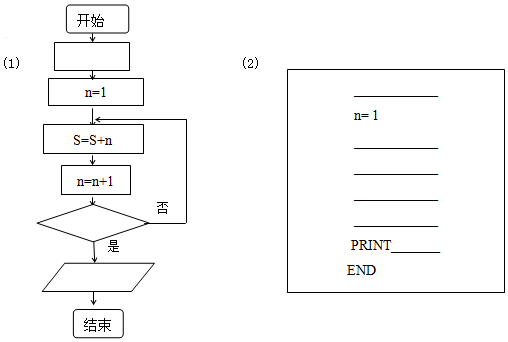
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4}^{n}-1}{3}$ | B. | $\frac{1-{4}^{n}}{3}$ | C. | $\frac{1{6}^{n}-1}{15}$ | D. | $\frac{1-1{6}^{n}}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=sinx,x∈[0,2π]是奇函数 | |
| B. | 函数y=2sin($\frac{π}{6}$-2x)在区间[-$\frac{π}{6},\frac{π}{3}$]上单调递减 | |
| C. | 函数y=2sin($\frac{π}{3}-2x$)-cos($\frac{π}{6}+2x$)(x∈R)的一条对称轴方程是x=$\frac{π}{6}$ | |
| D. | 函数y=sinπx•cosπx的最小正周期为2,且它的最大值为1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com