练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    直线l1：kx＋(1－k)y－3＝0和l2：(k－1)x＋(2k＋3)y－2＝0互相垂直，则k＝(　　)

    A．－3或－1           B．3或1

    C．－3或1             D．－1或3


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    给出平面区域G，如图所示，其中A(5,3)，B(2,1)，C(1,5)．若使目标函数P＝ax＋y(a＞0)取得最大值的最优解有无穷多个，则a的值为(　　)

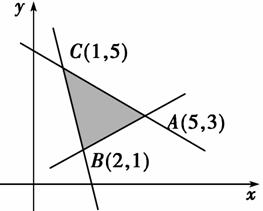
    A．4         B．2        C.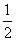          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数（为常数，是自然对数的底数），曲线在点处的切线与轴平行.

    （Ⅰ）求的值；

    （Ⅱ）求的单调区间；

    （Ⅲ）设,其中为的导函数.

    证明：对任意.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定点A，B，且|AB|＝4，动点P满足|PA|－|PB|＝3，则|PA|的最小值为(　　)

    A.        B.        C.        D．5

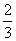
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线的方程是16x2－9y2＝144.

    (1)求双曲线的焦点坐标、离心率和渐近线方程；

    (2)设F1和F2是双曲线的左、右焦点，点P在双曲线上，且|PF1|·|PF2|＝32，求∠F1PF2的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直角坐标系中坐标原点O关于直线l：2xtan α＋y－1＝0的对称点为A(1,1)，则tan 2α的值为(　　)

    A．－         B.          C．1         D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两点A(2,3)，B(4,1)，直线l：x＋2y－2＝0，在直线l上求一点P.

    (1)使|PA|＋|PB|最小；

    (2)使|PA|－|PB|最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则的最大值为(　　)

    A．2       B．3         C．6        D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以正方体ABCDA1B1C1D1的棱AB，AD，AA1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系，且正方体的棱长为一个单位长度，则棱CC1的中点的坐标为(　　)

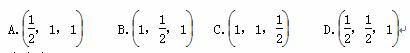
    查看答案和解析>>

    同步练习册答案